Угловой радиус – Определите линейный радиус Солнца (в радиусах Земли и километрах). Угловой радиус фотосферы и расстояние от Земли до Солнца Считайте известными.

Угловой размер — Википедия

Материал из Википедии — свободной энциклопедии

Угловой размер (иногда также угол зрения) — это угол между прямыми линиями, соединяющими диаметрально противоположные крайние точки измеряемого (наблюдаемого) объекта и глаз наблюдателя.

Под угловым размером может также пониматься не плоский угол, под которым виден объект, а телесный угол.

Если отрезок длиной D перпендикулярен линии наблюдения (более того, она является серединным его перпендикуляром) и находится на расстоянии L от наблюдателя, то точная формула для углового размера этого отрезка: 2arctg⁡D2L{\displaystyle 2\,\operatorname {arctg} {\frac {D}{2L}}}. Если размер тела D мал по сравнению с расстоянием от наблюдателя L, то угловой размер (в радианах) определяется отношением D/L, так как tg⁡α≈α{\displaystyle \operatorname {tg} \alpha \approx \alpha } для малых углов. При удалении тела от наблюдателя (увеличении L), угловой размер тела уменьшается.

Понятие углового размера очень важно в геометрической оптике, и в особенности применительно к органу зрения — глазу. Глаз способен регистрировать именно угловой размер объекта. Его реальный, линейный размер определяется мозгом по оценке расстояния до объекта и из сравнения с другими, уже известными телами.

Согласно геометрии предмет, удалённый от глаза на расстояние, в 57 раз большее его поперечника, должен представляться наблюдателю под углом почти в 1°.

Сравнение угловых размеров Солнца, Луны и планет. Размеры приведены в угловых минутах (‘) и секундах («) Иллюстрация приведена не в масштабе: для того, чтобы получить точное представление о размерах, нужно рассматривать это изображение с расстояния, в 102.6 раз превышающего ширину кружка «Moon: max.». Например, если диаметр этого кружка на вашем мониторе составляет 10 см, то смотреть следует с расстояния 10,26 м.

Угловой размер астрономического объекта, видимый с Земли, обычно называется угловым диаметром или видимым диаметром. Вследствие удалённости всех объектов, угловые диаметры планет и звёзд очень малы и измеряются в угловых минутах (′) и секундах(″). Например, средний видимый диаметр Луны равен 31′05″ (вследствие эллиптичности лунной орбиты угловой размер изменяется от 29′20″ до 33′32″), или ≈0,5∘.{\displaystyle \approx 0{,}5^{\circ }.} Средний видимый диаметр Солнца — 31′59″ (изменяется от 31′31″ до 32′36″)^[1]. Видимые диаметры звёзд чрезвычайно малы и лишь у немногих достигают нескольких сотых долей секунды.

Угловой диаметр — это… Что такое Угловой диаметр?



Угловой диаметр

Угловой размер — это угол между линиями, соединяющими диаметрально противоположные точки измеряемого объекта и глаз наблюдателя.

Под угловым размером может также пониматься не плоский угол, под которым виден объект, а телесный угол.

Если отрезок длиной D перпендикулярен линии наблюдения (более того, она является серединным его перпендикуляром) и находится на расстоянии L от наблюдателя, то точная формула для углового размера этого отрезка: . Если размер тела D мал по сравнению с расстоянием от наблюдателя L, то угловой размер (в радианах) определяется отношением D/L, так как для малых углов. При удалении тела от наблюдателя (увеличении L), угловой размер тела уменьшается.

Понятие углового размера очень важно в геометрической оптике, и в особенности применительно к органу зрения — глазу. Глаз способен регистрировать именно угловой размер объекта. Его реальный, линейный размер определяется мозгом по оценке расстояния до объекта и из сравнения с другими, уже известными телами.

В астрономии

Угловой размер астрономического объекта, видимый с Земли, обычно называется угловым диаметром или видимым диаметром. Вследствие удалённости всех объектов, угловые диаметры планет и звёзд очень малы и измеряются в угловых минутах (′) и секундах(″). Например, средний видимый диаметр Луны равен 31′05″ (вследствие эллиптичности лунной орбиты угловой размер изменяется от 29′24″ до 33′40″). Средний видимый диаметр Солнца — 31′59″ (изменяется от 31′27″ до 32′31″). Видимые диаметры звёзд чрезвычайно малы и лишь у немногих светил достигают нескольких сотых долей секунды.

См. также

Wikimedia Foundation. 2010.

• Угловое увеличение
• Угловой (футбол)

Смотреть что такое «Угловой диаметр» в других словарях:

• УГЛОВОЙ ДИАМЕТР — УГЛОВОЙ ДИАМЕТР, в астрономии видимый диаметр небесного тела, выраженный в угловых мерах (обычно в дуговых градусах и минутах). Это угол, вершиной которого является глаз наблюдателя, а основанием видимый диаметр наблюдаемого тела. Если известно… …   Научно-технический энциклопедический словарь

• угловой диаметр — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN angular diameter …   Справочник технического переводчика

• Угловой диаметр — Видимый диаметр объекта, измеряемый в угловых единицах, т.е. в радианах, градусах, дуговых минутах или секундах. Угловой диаметр зависит как от истинного диаметра, так и от расстояния до объекта …   Астрономический словарь

• угловой диаметр — kampinis skersmuo statusas T sritis fizika atitikmenys: angl. angular diameter; apparent diameter vok. scheinbare Durchmesser, m; Winkeldurchmesser, m rus. видимый диаметр, m; угловой диаметр, m pranc. diamètre angulaire, m; diamètre apparent, m …   Fizikos terminų žodynas

• угловой диаметр приемника — (η2) Угол, под которым наблюдается наибольший размер видимой площади приемника из исходного центра (β1 = β2 = 0°). [ГОСТ Р 41.104 2002] Тематики автотранспортная техника …   Справочник технического переводчика

• угловой диаметр светоотражающего образца

  — (η1) Угол, под которым наблюдается наибольший размер видимой площади светоотражающего образца либо из центра источника света, либо из центра приемника (β1 = β2 = 0°). [ГОСТ Р 41.104 2002] Тематики автотранспортная техника …   Справочник технического переводчика

• угловой диаметр приемника (η₂) — 2.4.3 угловой диаметр приемника (η2): Угол, под которым наблюдается наибольший размер видимой площади приемника из исходного центра (b1 = b2 = 0°). Источник …   Словарь-справочник терминов нормативно-технической документации

• угловой диаметр светоотражающего образца (η₁) — 2.4.2 угловой диаметр светоотражающего образца (η1): Угол, под которым наблюдается наибольший размер видимой площади светоотражающего образца либо из центра источника света, либо из центра приемника (b1 = b2 = 0°). Источник …   Словарь-справочник терминов нормативно-технической документации

• Диаметр — в изначальном значении это отрезок, соединяющий две точки на окружности и проходящий через центр окружности, а также длина этого отрезка. Диаметр равен двум радиусам. Содержание 1 Диаметр геометрических фигур …   Википедия

• Диаметр Солнца и планет — поперечник видимого диска этих светил, выраженный в угловой мере. Зная видимый диаметр и расстояние от Земли, легко вычислить истинные размеры светил. Угловой диаметр изменяется в зависимости от расстояния, и так как все движения светил относятся …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Угловое расстояние — Википедия

Материал из Википедии — свободной энциклопедии

В математике (в частности, в геометрии и тригонометрии) и во всех естественных науках (например, в астрономии и геофизике) угловое расстояние — это мера видимого расстояния между двумя точками или объектами, выраженная в угловых единицах дуги, при условии, что наблюдатель находится в вершине угла концами которого являются две рассматриваемые точки. Угловой диаметр является частным случаем углового размера.

Угловое расстояние является фундаментальной величиной в астрономии, определяющей положение любого объекта на небесной сфере по его небесным координатам: либо в угловых единицах, либо во времени. Азимут, высота, склонение или прямое восхождение объекта на небе, среди прочего, являются небесными координатами. Любое из них — это угловое расстояние до точки или плоскости отсчета: горизонта, небесного экватора, меридиана и т. д.

Термин угловое расстояние технически синонимичен самому углу, но предназначен для обозначения линейного расстояния (часто огромного и неизвестного) между этими объектами (например, звездами, наблюдаемыми с Земли).

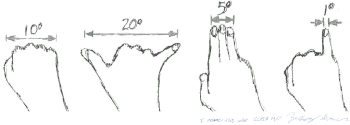
Для визуальных наблюдений без претензий на точность можно вычислить угловое расстояние, конечно, с приближениями порядка степени, и, конечно, очень грубо.

Отдельные вариации — длина руки, толщина пальцев и т. д. — меняют значения в первых приближениях, но не так важны для определения местоположения звезды или планеты, видимой невооруженным глазом или для связи созвездия с соседями.

Поскольку угловое расстояние концептуально совпадает с углом, оно измеряется в тех же единицах, например, градусах или радианах и с использованием таких приборов, как гониометры или оптические приборы, специально предназначенные для поворота в четко определенных направлениях и записи соответствующих углов (такие как телескопы).

Чтобы рассчитать угловое расстояние θ в угловых секундах для двойной звёздные системы, экзопланеты, объекта Солнечной системы и других астрономических объектов, используется размер большой полуоси, выраженной в астрономических единицах (а.е.), деленное на расстояние D, выраженное в парсеках, согласно формуле для малых углов — tan⁡(aD){\displaystyle \tan({\frac {a}{D}})}:

θ≈aD{\displaystyle \theta \approx {\dfrac {a}{D}}}

Учитывая два угловых положения, каждое из которых определяется прямым восхождением (RA), α∈[0,2π]{\displaystyle \alpha \in [0,2\pi ]} и склонением (dec), δ∈[−π/2,π/2]{\displaystyle \delta \in [-\pi /2,\pi /2]} угловое расстояние между двумя точками можно рассчитать, используя следующую формулу:

θ=cos−1⁡[sin⁡(δ1)sin⁡(δ2)+cos⁡(δ1)cos⁡(δ2)cos⁡(α1−α2)]{\displaystyle \theta =\cos ^{-1}\left[\sin(\delta _{1})\sin(\delta _{2})+\cos(\delta _{1})\cos(\delta _{2})\cos(\alpha _{1}-\alpha _{2})\right]}

Угловой размер, линейный размер и расстояние

Угловой размер — это угол между линиями, соединяющими диаметрально противоположные точки измеряемого объекта и глаз наблюдателя.
Посмотрим на рисунок: здесь отрезок D — измеряемый объект, отрезок L — линия наблюдения, перпендикулярная отрезку D и являющаяся его серединным перпендикуляром, и угол а — угловой размер отрезка D.
Очевидные соотношения между величинами (вспомним тригонометрию):

Таким образом, наблюдатель, зная, например, линейный размер объекта, по угловому размеру объекта может определить расстояние до него. Помню, раньше для этих целей военные бинокли снабжали специальными риcками для определения углового размера.

Ну и обратные задачи тоже имеют место — зная, например, расстояние и линейный размер объекта, можно определить его угловой размер; и наконец, зная расстояние и угловой размер, можно определить линейный размер. Последние задачи актуальны для астрономии. Там используют термин угловой диаметр — то есть видимый диаметр небесного тела, выраженный в угловых мерах.

Ниже калькуляторы, рассчитывающие неизвестные по всем соотношениям. В качестве данных по умолчанию используется расстояние от Земли до Солнца, диаметр Солнца и средний угловой диаметр Солнца, наблюдаемого с Земли.

Расстояние по угловому и линейному размеру

Угловой размерТочность вычисления

Знаков после запятой: 2

save Сохранить share Поделиться extension Виджет

Линейный размер по угловому размеру и расстоянию

Угловой размерТочность вычисления

Знаков после запятой: 2

Линейный размер

 

save Сохранить share Поделиться extension Виджет

Угловой размер по расстоянию и линейному размеру

Угловой размер

 

save Сохранить share Поделиться extension Виджет

угловой радиус — это… Что такое угловой радиус?



угловой радиус

мат. angular radius

Большой англо-русский и русско-английский словарь. 2001.

• угловой профиль
• угловой ротор

Смотреть что такое «угловой радиус» в других словарях:

• Радиус качения шины — отношение продольной составляющей поступательной скорости колеса к его угловой скорости;… Источник: Решение Совета Евразийской экономической комиссии от 20.07.2012 N 60 О принятии технического регламента Таможенного союза О безопасности… …   Официальная терминология

• Угловой момент — Момент импульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси… …   Википедия

• эффективный радиус гидрофона a_h, a_h3, a_h6, — 3.10 эффективный радиус гидрофона ah, ah4, ah6, м: Радиус гидрофона в виде жесткого диска, который имеет расчетную диаграмму направленности, угловой сектор которой равен угловому сектору измеренной диаграммы направленности рассматриваемого… …   Словарь-справочник терминов нормативно-технической документации

• эффективный радиус гидрофона a_h, a_h3, a_h6, м — 3.21 эффективный радиус гидрофона ah, ah4, ah6, м: Радиус гидрофона в виде жесткого диска, который имеет расчетную диаграмму направленности, угловой сектор которой равен угловому сектору измеренной диаграммы направленности рассматриваемого… …   Словарь-справочник терминов нормативно-технической документации

• Вега — У этого термина существуют и другие значения, см. Вега (значения). Вега Звезда …   Википедия

• Vega — Вега Звезда Положение Веги в созвездии Лиры История исследования Обозначения Vega, α Lyr, 3 Lyr, HIP 91262[1], GCRV 11085 …   Википедия

• Вега (звезда) — Вега Звезда Положение Веги в созвездии Лиры История исследования Обозначения Vega, α Lyr, 3 Lyr, HIP 91262[1], GCRV 11085 …   Википедия

• Радуга* — всем известное оптическое явление в атмосфере; наблюдается, когда солнце освещает пелену падающего дождя и наблюдатель находится между солнцем и дождем. Явление это представляется в виде одной, реже двух концентрических светлых дуг, рисующихся на …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

• Радуга — всем известное оптическое явление в атмосфере; наблюдается, когда солнце освещает пелену падающего дождя и наблюдатель находится между солнцем и дождем. Явление это представляется в виде одной, реже двух концентрических светлых дуг, рисующихся на …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

• Радуга — У этого термина существуют и другие значения, см. Радуга (значения). Радуга над Ладожским озером …   Википедия

• Цвета радуги — Радуга над Ладожским озером Радуга атмосферное оптическое и метеорологическое явление, наблюдаемое обычно после дождя или перед ним. Оно выглядит как дуга или окружность, составленная из цветов спектра. Глядя снаружи внутрь дуги: красный,… …   Википедия

Окружность — Википедия

Окружность (C), её центр (O), радиус (R) и диаметр (D)

Окру́жность — замкнутая плоская кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки^[1]: эта точка называется центром окружности. Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом; радиусом называется также и длина этого отрезка. Окружность разбивает плоскость на две части^[2] — конечную внутреннюю и бесконечную внешнюю. Внутренность окружности называется кругом; граничные точки (то есть саму окружность) в зависимости от подхода, круг может включать или не включать.

Построение окружности циркулем

Практическое построение окружности возможно с помощью циркуля.

Окружность нулевого радиуса (вырожденная окружность) является точкой, далее этот случай исключается из рассмотрения, если не оговорено иное.

Окружность называется единичной, если её радиус равен единице. Единичная окружность является одним из основных объектов тригонометрии.

Далее всюду буква R{\displaystyle R} обозначает радиус окружности.

Прямая может иметь с окружностью не более двух общих точек.

Прямая, пересекающая окружность в двух различных точках, называется секущей. Отрезок секущей, расположенный внутри окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром; тот же термин используется для его длины. Диаметр вдвое больше радиуса: D=2R,{\displaystyle D=2R,} он делит окружность на две равные части и поэтому является её осью симметрии. Диаметр больше любой другой хорды^[3].

Хорда разбивает круг на две части, называемые сегментами круга. Два различных радиуса тоже разбивают круг на две части, называемые секторами круга (см. рисунки)^[3].

Любые две несовпадающие точки окружности делят её на две части. Каждая из этих частей называется дугой окружности. Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.

Для заданной окружности имеют место следующие свойства^[3].

• Хорды, равноотстоящие от центра, равны. Обратно, если две хорды равны по длине, то они одинаково удалены от центра.
• Равным хордам соответствуют равные дуги, и наоборот.

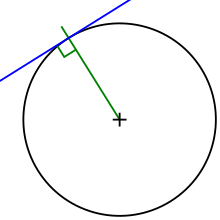
Прямая, имеющая с окружностью ровно одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. Касательная к окружности всегда перпендикулярна её радиусу (и диаметру), проведенному в точке касания. То есть радиус является одновременно и нормалью к окружности

[4].

Отрезки касательных к окружности, проведённых из одной точки, не лежащей на окружности, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности^[5].

• 

  Вписанный угол θ равен половине величины центрального угла 2θ, опирающегося на ту же самую дугу (розового цвета)

• 

  К расчёту длины дуги и хорды

Центральный угол — угол с вершиной в центре окружности. Центральный угол может быть принят как угловая мера дуги, на которую он опирается. Центральный угол, образуемый дугой окружности, равной по длине радиусу, в математике принимается в качестве единицы измерения углов, и называется радиан.

Из определения радиана следует, что длина L{\displaystyle L} любой дуги окружности связана с центральным углом θ{\displaystyle \theta }, опирающимся на эту дугу, простым соотношением^[6]: L=Rθ.{\displaystyle L=R\theta .} (при этом длина хорды, стягивающей ту же дугу, равна 2Rsin⁡θ2<L{\displaystyle 2R\sin {\theta \over 2}<L}). Поскольку длина окружности равна 2πR{\displaystyle 2\pi R}, с ростом угла значение его радианной меры меняется от 0 до 2π.{\displaystyle 2\pi .}

Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.

Внешний угол для вписанного угла

— угол, образованный одной стороной и продолжением другой стороны вписанного угла (угол θ коричневого цвета на рис.). Внешний угол для вписанного угла равен вписанному углу, опирающемуся на ту же хорду с другой стороны.

Угол между окружностью и прямой — угол между секущей прямой и одной из двух касательных к окружности в точке пересечения прямой и окружности.

Свойства вписанных углов:

• Вписанный угол либо равен половине центрального угла, опирающегося на его дугу, либо дополняет половину этого угла до 180°. Вписанный угол, опирающийся на дугу длиной в половину окружности, всегда прямой (равен 90°).
• Вписанный угол не меняет своей величины при перемещении его вершины вдоль окружности.
• Два вписанных угла, опирающиеся на одну и ту же дугу, равны.

Другие свойства:

• Угол между двумя секущими, проведёнными из точки, лежащей вне окружности, равен полуразности мер дуг, лежащих между секущими.
• Угол между пересекающимися хордами равен полусумме мер дуги, лежащей в угле, и дуги напротив неё.
• Угол между касательной и хордой, имеющими общую точку, равен половине угловой меры дуги, стягиваемой хордой.

• Изопериметрическое неравенство: Из всех замкнутых кривых данной длины окружность ограничивает область максимальной площади.
• Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
• Говорят, что две окружности касаются, если они имеют единственную общую точку. Точка касания двух окружностей лежит на прямой, проходящей через их центры.
• Теорема о секущих: Если через произвольную точку E{\displaystyle E} проведена секущая, то произведение расстояний от этой точки до точек пересечения секущей с окружностью не зависит от выбора секущей (и равно абсолютной величине степени точки относительно окружности). Если точка E{\displaystyle E} лежит вне окружности, то из нее к окружности можно провести касательную. Квадрат длины отрезка касательной до точки касания будет равен той же величине.

• Как частный случай предыдущего, при пересечении двух хорд в произвольной точке E{\displaystyle E} получаются отрезки, произведение длин которых у одной хорды равно соответствующему произведению у другой (см. рисунок), т. е. AE⋅EB=CE⋅ED{\displaystyle AE\cdot EB=CE\cdot ED}.

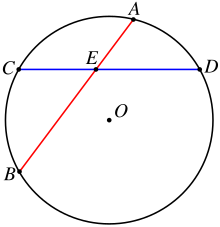AE⋅EB=CE⋅ED{\displaystyle AE\cdot EB=CE\cdot ED} Если радиус круга равен 1, то его окружность равна 2π.

Длина окружности:

C=2πR=πD.{\displaystyle C=2\pi R=\pi D.}

Радиус окружности:

R=C2π=D2.{\displaystyle R={\frac {C}{2\pi }}={\frac {D}{2}}.}

Диаметр окружности:

D=Cπ=2R.{\displaystyle D={\frac {C}{\pi }}=2R.}

Площадь круга радиуса R:

S=πR2=πD24.{\displaystyle S=\pi R^{2}={\frac {\pi D^{2}}{4}}.}

Площадь сектора, ограниченного центральным углом α, измеряемым в градусах, радиусом R:

S=πR2α360∘.{\displaystyle S=\pi R^{2}{\frac {\alpha }{360^{\circ }}}.}

Площадь сегмента, ограниченного дугой окружности, центральным углом α, хордой:

S=πR2α360∘−R2sin⁡α2.{\displaystyle S=\pi R^{2}{\frac {\alpha }{360^{\circ }}}-{\frac {R^{2}\sin \alpha }{2}}.}

Окружность, наряду с прямой, является самой распространённой кривой практически во всех областях человеческой деятельности. История её исследования и применения уходит в глубокую древность; особенную важность придало этой теме изобретение колеса. Античные учёные рассматривали прямые и окружности как единственный пример «совершенных» кривых, поэтому в геометрии считались допустимыми только построения с помощью циркуля и линейки, а движение планет моделировалось как наложение вращений по окружностям. Теории окружностей посвящена III книга «Начал» Евклида.

Также в древности было открыто, что отношение длины окружности к её диаметру (число π) одно и то же для всех окружностей. Исторически важной темой многовековых исследований было уточнение этого отношения, а также попытки решить проблему «квадратуры круга». В дальнейшем развитие теории окружностей привело к созданию тригонометрии, теории колебаний и многих других практически важных разделов науки и техники.

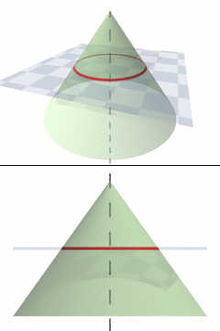Окружность получается как сечение конуса плоскостью, перпендикулярной его оси

Аналитическая геометрия окружностей[править | править код]

С точки зрения аналитической геометрии, окружность является простой плоской алгебраической кривой второго порядка. Окружность является частным случаем эллипса, у которого полуоси равны, и поэтому окружность относится к коническим сечениям.

Декартовы координаты[править | править код]

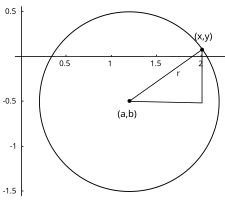Окружность радиуса r = 1, центр (a, b) = (1.2, −0.5)

Общее уравнение окружности записывается как:

x2+y2+Ax+By+C=0,{\displaystyle x^{2}+y^{2}+Ax+By+C=0,}

или

(x−x0)2+(y−y0)2=R2,{\displaystyle \left(x-x_{0}\right)^{2}+\left(y-y_{0}\right)^{2}=R^{2},}

где

2×0=−A,2y0=−B,2R=A2+B2−4C.{\displaystyle 2x_{0}=-A,\;2y_{0}=-B,\;2R={\sqrt {A^{2}+B^{2}-4C}}.}

Точка (x0,y0){\displaystyle \left(x_{0},y_{0}\right)} — центр окружности, R{\displaystyle R} — её радиус.

Уравнение окружности радиуса R{\displaystyle R} с центром в начале координат:

x2+y2=R2.{\displaystyle x^{2}+y^{2}=R^{2}.}

Уравнение окружности, проходящей через точки (x1,y1),(x2,y2),(x3,y3),{\displaystyle \left(x_{1},y_{1}\right),\left(x_{2},y_{2}\right),\left(x_{3},y_{3}\right),} не лежащие на одной прямой (с помощью определителя):

|x2+y2xy1x12+y12x1y11x22+y22x2y21x32+y32x3y31|=0.{\displaystyle {\begin{vmatrix}x^{2}+y^{2}&x&y&1\\x_{1}^{2}+y_{1}^{2}&x_{1}&y_{1}&1\\x_{2}^{2}+y_{2}^{2}&x_{2}&y_{2}&1\\x_{3}^{2}+y_{3}^{2}&x_{3}&y_{3}&1\end{vmatrix}}=0.}

Тогда в явном виде координаты центра окружности определяются по формулам:

x0=−12y1(x22+y22−x32−y32)+y2(x32+y32−x12−y12)+y3(x12+y12−x22−y22)x1(y2−y3)+x2(y3−y1)+x3(y1−y2){\displaystyle x_{0}=-{\frac {1}{2}}{\frac {y_{1}(x_{2}^{2}+y_{2}^{2}-x_{3}^{2}-y_{3}^{2})+y_{2}(x_{3}^{2}+y_{3}^{2}-x_{1}^{2}-y_{1}^{2})+y_{3}(x_{1}^{2}+y_{1}^{2}-x_{2}^{2}-y_{2}^{2})}{x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})}}}

y0=12×1(x22+y22−x32−y32)+x2(x32+y32−x12−y12)+x3(x12+y12−x22−y22)x1(y2−y3)+x2(y3−y1)+x3(y1−y2){\displaystyle y_{0}={\frac {1}{2}}{\frac {x_{1}(x_{2}^{2}+y_{2}^{2}-x_{3}^{2}-y_{3}^{2})+x_{2}(x_{3}^{2}+y_{3}^{2}-x_{1}^{2}-y_{1}^{2})+x_{3}(x_{1}^{2}+y_{1}^{2}-x_{2}^{2}-y_{2}^{2})}{x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})}}}

Окружность также можно описать с помощью параметрического уравнения:

{x=x0+Rcos⁡φy=y0+Rsin⁡φ,0⩽φ<2π.{\displaystyle {\begin{cases}x=x_{0}+R\cos \varphi \\y=y_{0}+R\sin \varphi \end{cases}},\;\;\;0\leqslant \varphi <2\pi .}

В декартовой системе координат окружность не является графиком функции, но она может быть описана как объединение графиков двух следующих функций:

y=y0±R2−(x−x0)2.{\displaystyle y=y_{0}\pm {\sqrt {R^{2}-(x-x_{0})^{2}}}.}

Если центр окружности совпадает с началом координат, функции принимают вид:

y=±R2−x2.{\displaystyle y=\pm {\sqrt {R^{2}-x^{2}}}.}

Полярные координаты[править | править код]

Окружность радиуса R{\displaystyle R} с центром в точке (ρ0,ϕ0){\displaystyle \left(\rho _{0},\phi _{0}\right)}:

ρ2−2ρρ0cos⁡(ϕ−ϕ0)+ρ02=R2.{\displaystyle \rho ^{2}-2\rho \,\rho _{0}\cos \left(\phi -\phi _{0}\right)+\rho _{0}^{2}=R^{2}.}

Если полярные координаты центра окружности ρ0=R,ϕ0=α,{\displaystyle \rho _{0}=R,\;\phi _{0}=\alpha ,} то проходящая через начало координат окружность описывается уравнением:

ρ(φ)=2Rcos(φ−α),α−π2⩽φ⩽α+π2.{\displaystyle \rho (\varphi )=2R\cos \,(\varphi -\alpha ),\;\;\;\alpha -{\frac {\pi }{2}}\leqslant \varphi \leqslant \alpha +{\frac {\pi }{2}}.}

Если же центр является началом координат, то уравнение будет иметь вид

ρ=R.{\displaystyle \rho =R.}

Комплексная плоскость[править | править код]

На комплексной плоскости окружность задаётся формулой:

|z−z0|=R{\displaystyle \left|z-z_{0}\right|=R}

или в параметрическом виде

z=z0+Reit,t∈R.{\displaystyle z=z_{0}+Re^{it},\,t\in \mathbb {R} .}

Окружности в пространстве[править | править код]

В пространстве окружность радиуса R{\displaystyle R} с центром в точке M0(x0,y0,z0){\displaystyle M_{0}(x_{0},y_{0},z_{0})} можно определить как контур диаметрального сечения сферы

(x−x0)2+(y−y0)2+(z−z0)2=R2{\displaystyle (x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=R^{2}}

плоскостью

a⋅(x−x0)+b⋅(y−y0)+c⋅(z−z0)=0{\displaystyle a\cdot (x-x_{0})+b\cdot (y-y_{0})+c\cdot (z-z_{0})=0},

где a,b,c{\displaystyle a,b,c} — параметры, не равные одновременно нулю; то есть все точки, лежащие на данной окружности, есть решения системы

{(x−x0)2+(y−y0)2+(z−z0)2=R2,a⋅(x−x0)+b⋅(y−y0

Угловой размер — Карта знаний

• Угловой размер (иногда также угол зрения) — это угол между прямыми линиями, соединяющими диаметрально противоположные крайние точки измеряемого (наблюдаемого) объекта и глаз наблюдателя.

  Под угловым размером может также пониматься не плоский угол, под которым виден объект, а телесный угол.

Источник: Википедия

Связанные понятия

Фазовый угол (англ. Phase angle) — угол между падающим на наблюдаемый объект светом и отражённым от объекта светом, получаемым наблюдателем. В рамках астрономических наблюдений обычно является углом в системе Солнце-объект-наблюдатель. Углово́е по́ле объекти́ва в простра́нстве предме́тов — плоский угол между двумя лучами, проходящими через центр входного зрачка объектива к наиболее удалённым от оптической оси точкам объекта в пространстве предметов, отображающимся на противоположных краях кадрового окна (полевой диафрагмы). При фиксированных размерах кадрового окна угловое поле обратно пропорционально фокусному расстоянию. У́гол — геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (которая называется вершиной угла). Большая полуось — один из основных геометрических параметров объектов, образованных посредством конического сечения.

Упоминания в литературе

На рисунке 23 представлены результаты опытов Гальвея и Боринга по вопросу о зависимости видимого размера предмета от его расстояния. Предметом служил светящийся диск, угловые размеры которого все время оставались постоянными, расстояние же от наблюдателя менялось в пределах от 3 до 36 м. Видимый размер сравнивался с другим светящимся диском, находившимся на постоянном расстоянии в 3 м. Диаметр этого диска менялся измеримым образом так, чтобы он как раз равнялся первому, наблюдаемому диску. Если бы мозг не вносил никаких автоматических поправок в размеры изображения на сетчатке, то, ввиду того что угловые размеры первого диска оставались всегда постоянными, следовало бы ожидать, что на рисунке 23, на котором по оси абсцисс отложено расстояние в метрах, а по ординатам – воспринимаемый нами размер в сантиметрах, мы получим неизменную прямую, параллельную оси абсцисс (она нанесена штриховой линией). В действительности получается совсем иное. При наблюдении последовательно сразу двумя глазами, одним глазом и через длинную тонкую трубку получаются наклонные прямые. Этот наклон уменьшается по мере устранения видимости окружающих предметов. На рис. 4 приведен профиль линии ОН, излучаемый этим источником. Как видим, он состоит из большого количества узких ярких линий. Каждой линии соответствует определенная скорость движения по лучу зрения излучающего эту линию облака. Величина этой скорости определяется эффектом Доплера. Различие скоростей (по лучу зрения) между различными облаками достигает – 10 км/с. Упомянутые выше интерферометрические наблюдения показали, что облака, излучающие каждую линию, пространственно не совпадают. Картина получается такая: внутри области размером приблизительно 1,5 секунды дуги движутся с разными скоростями около 10 компактных облаков. Каждое облако излучает одну определенную (по частоте) линию. Угловые размеры облаков очень малы, порядка нескольких тысячных секунды дуги. Так как расстояние до туманности W3 известно (около 2000 пк), то угловые размеры легко могут быть переведены в линейные. Оказывается, что линейные размеры области, в которой движутся облака, порядка 10-2 пк, а размеры каждого облака всего лишь на порядок величины больше расстояния от Земли до Солнца. ? острота зрения – способность глаза различать мелкие детали предметов. Размеры предметов выражаются в угловых величинах, которые связаны с линейными размерами по формуле tg α/2 = h/2L, где α – угловой размер объекта, h – линейный размер, L – расстояние от глаза до объекта. • острота зрения – способность глаза различать мелкие детали предметов. Размеры предметов выражаются в угловых величинах, которые связаны с линейными размерами по формуле tg α/2 = h/2L, где α – угловой размер объекта, h – линейный размер, L – расстояние от глаза до объекта. У людей с нормальным зрением пространственный порог остроты зрения равен одной угловой минуте; минимально допустимые размеры элементов отображения, предъявляемые человеку, должны быть на уровне оперативного порога и составлять не менее 15 угловых минут. Однако это справедливо только для предметов простой формы. Для сложных предметов, опознание которых ведется по внешним и внутренним признакам, оптимальные условия будут в том случае, если их размеры составляют не менее 30–40 угловых минут; Видимая площадь созвездия определяется телесным углом, который оно занимает на небе. Обычно эту площадь указывают в квадратных градусах. Для неастрономов такая единица непривычна. Чтобы сделать ее наглядной, нужно вытянуть вперед руку с поднятым указательным пальцем: его ноготь как раз покроет на небе площадку примерно в 1 квадратный градус (линейный размер ногтя 1 см х 1 см, а его расстояние от глаза составляет около 57 см, поэтому угловой размер ногтя – примерно 1°х1°). Диски Луны или Солнца занимают на небе площадь около 0,2 кв. градуса, а площадь всей небесной сферы составляет около 41 253 кв. градусов. Именно такую площадь покрывают в сумме все 88 созвездий; они целиком занимают небо, свободных мест между ними нет. В среднем на одно созвездие приходится площадь около 470 кв. градусов, или 2344 лунных дисков. Но площади реальных созвездий сильно различаются. Самое большое из них, Гидра, не отличается популярностью даже среди любителей астрономии, хотя его площадь на небе почти в 20 раз больше, чем самого маленького, но широко известного созвездия Южный Крест. Популярность созвездия определяется не его площадью, а количеством в нем ярких звезд и интересных объектов. Впрочем, даже на маленькой территории Южного Креста легко разместились бы около трех сотен полных лунных дисков! Данные о линейных размерах НЛО, сообщаемые очевидцами, в ряде случаев весьма относительны, так как при визуальном наблюдении можно определить с достаточной точностью только угловые размеры объекта. Первоначально координаты трека анализируются независимо друг от друга. Каждый временной ряд аппроксимируется кусочной ступенчатой функцией (Lemire, 2007), разбивающей последовательность на интервалы, в пределах которых координата не изменяется или изменяется незначительно. Пересечения полученных интервалов во времени определяют положения фиксаций на треке (рисунок 3). Восстановление положения фиксаций на экране монитора проводится с помощью отображающей функции по координатам, полученным из усреднения измерений на выделенных временных интервалах. Угловое изменение направления взора между двумя последовательными фиксациями определяет амплитуду саккады. В случае, когда амплитуда не превышает 1,4°, две последовательные фиксации объединяются в одну. Выбор данного критерия многократно обсуждался в литературе (Velichkovsky et al., 2005) и может быть обусловлен целями эксперимента, а также анатомо-физиологическими свойствами сетчатки. Так, известно, что угловой размер фовеа глаза человека составляет около 2°. Примером причины выбора иного амплитудного критерия, обусловленного целями эксперимента, может быть, например, необходимость оценки стабильности фиксации взора на одной точке длительное время. В этом случае критичными могут быть также микросаккады и дрейф. Отметим также, что в программе предусмотрена возможность опциональной настройки данного критерия. Солнце имеет радиус около 696 000 км, масса его составляет примерно 2×1030 кг. Температура поверхности составляет 5800 К, а светимость (мощность солнечного излучения) – 3,86×1026 Дж/с. Расстояние от Земли до Солнца составляет примерно 150 млн км, свет проходит его за 8 минут с небольшим. На небе Солнце имеет угловой размер около половины градуса. Возраст Солнца равен примерно 4,6 млрд лет, а полная продолжительность его жизни составляет около 12 млрд лет. В конце своего пути, пройдя стадию красного гиганта и «горения» гелия в ядре, наша звезда станет углеродно-кислородным белым карликом. Угловые размеры освещенных участков рассматриваемого объекта при крайних настройках осветителя составляют 35′ и 1,7°.

Связанные понятия (продолжение)

Время свободного падения — характерное время, которое потребуется телу для коллапса под действием силы тяготения, если никакие другие силы не противодействуют коллапсу. Играет важную роль при определении временных шкал ряда астрофизических процессов, таких как звездообразование, вспышки сверхновых звёзд. Картографи́ческая прое́кция — математически определенный способ отображения поверхности Земли (либо другого небесного тела, или в общем смысле, любой искривлённой поверхности) на плоскость. Абсолютная звёздная величина — физическая величина, характеризующая светимость астрономического объекта. Для разных типов объектов используются разные определения абсолютной величины. Звёздный интерферо́метр Ма́йкельсона — прибор, позволяющий измерять угловые размеры звёзд и расстояния между двойными звёздами, а также изучить распределение интенсивности свечения на их поверхности методом интерференции. Один из первых проектов астрономических интерферометр, которые были воплощены «в железе». Потемнение диска к краю — оптический эффект при наблюдении звёзд, включая Солнце, при котором центральная часть диска звезды кажется ярче, чем край или лимб диска. Понимание данного эффекта позволило создать модели звездных атмосфер с учетом подобного градиента яркости, что способствовало развитию теории переноса излучения. Гравитацио́нный ра́диус (или ра́диус Шва́рцшильда) представляет собой характерный радиус, определённый для любого физического тела, обладающего массой: это радиус сферы, на которой находился бы горизонт событий, создаваемый этой массой (с точки зрения ОТО), если бы она была распределена сферически-симметрично, была бы неподвижной (в частности, не вращалась, но радиальные движения допустимы), и целиком лежала бы внутри этой сферы. Введен в научный обиход немецким ученым Карлом Шварцшильдом в… Гелиометр (от др.-греч. Ἥλιος или Ἠέλιος — солнце и métron — мера) — астрометрический инструмент для измерения небольших (до 1°) углов на небесной сфере. Название его происходит от первоначального способа применения — измерения диаметра Солнца. Позже использовался для измерения поперечников Луны, планет, планетоцентрических координат спутников планет, а также для измерения двойных звёзд и для определения параллаксов звёзд. Эллиптическая орбита — в астродинамике и небесной механике кеплерова орбита с эксцентриситетом меньше 1. Круговая орбита является частным случаем эллиптической орбиты при нулевом эксцентриситете. В более строгом определении эллиптической орбиты круговые орбиты исключаются; таким образом, эллиптические орбиты имеют эксцентриситет строго больше нуля и меньше единицы. В более широком смысле эллиптической орбитой является кеплерова орбита с отрицательной энергией. Такое определение включает и радиальные… Звёздная величина́ (блеск) — безразмерная числовая характеристика яркости объекта, обозначаемая буквой m (от лат. magnitudo «величина, размер»). Обычно понятие применяется к небесным светилам. Звёздная величина характеризует поток энергии от рассматриваемого светила (энергию всех фотонов в секунду) на единицу площади. Таким образом, видимая звёздная величина зависит и от физических характеристик самого объекта (то есть светимости), и от расстояния до него. Чем меньше значение звёздной величины, тем… Координаты Борна в специальной теории относительности — система координат, применяемая для описания вращающейся окружности или (в более общем смысле) диска. Фундамента́льная пло́скость — множество двумерных корреляционных соотношений, связывающих некоторые свойства нормальных эллиптических галактик, такие как радиус, светимость, масса, дисперсия скоростей, металличность, поверхностная яркость, цвет, плотность (светимости, массы, фазовая плотность), и, в меньшей степени, вид радиальных профилей поверхностной яркости. Обычно фундаментальную плоскость выражают в виде соотношения между эффективным радиусом, средней поверхностной яркостью и центральной дисперсией… Трикветрум (от лат. triquetrus — треугольный) (трикветр, линейка параллактическая) — древний астрономический угломерный инструмент, применявшийся для измерения зенитных расстояний небесных светил и параллакса Луны. Применение трикветра было описано Птолемеем в «Альмагесте» (V.12; ок. 140 года) и Коперником в книге «О вращении небесных сфер» (IV.15; 1543 год). Круговая орбита — орбита, все точки которой находятся на одинаковом расстоянии от центральной точки, создаваемая обращающимся вокруг неподвижной оси телом. Может рассматриваться как частный случай эллиптической орбиты при нулевом эксцентриситете. В Солнечной системе почти круговые орбиты у Венеры (эксцентриситет 0,0068) и Земли (эксцентриситет 0,0167). Для большинства пронумерованных астероидов известны всего несколько физических параметров. Всего несколько сотен астероидов имеют собственные страницы в Википедии, на которых содержится название, обстоятельства открытия, таблица элементов орбиты и ожидаемые физические характеристики.

Подробнее: Стандартные физические характеристики астероида

Сфери́ческая аберра́ция — аберрация оптических систем из-за несовпадения фокусов для лучей света, проходящих на разных расстояниях от оптической оси. Приводит к нарушению гомоцентричности пучков лучей от точечного источника, без нарушения симметрии строения этих пучков (в отличие от комы и астигматизма). Различают сферическую аберрацию третьего, пятого и высшего порядков. Динамический параллакс — метод определения параллакса и расстояния до визуально-двойной звезды, использующий сведения о массах компонентов двойной звезды, радиус орбиты и период обращения звёзд по орбите.Для определения расстояния до визуально-двойной звезды необходимо измерить угловую величину большой полуоси орбиты звезд и видимую звёздную величину. Применяя третий закон Кеплера в обобщённом виде, согласно которому произведение полной массы двойной системы и квадрата орбитального периода пропорционально… Радиальная траектория — в астродинамике и небесной механике кеплерова орбита с нулевым угловым моментом. Два объекта, находящиеся на радиальной траектории, движутся по одной прямой линии. Сфери́ческий сегме́нт — поверхность, часть сферы, отсекаемая от неё некоторой плоскостью. Плоскость отсекает два сегмента: меньший сегмент называется также сферическим кругом. Космологическое (метагалактическое) красное смещение — наблюдаемое для всех далёких источников (галактики, квазары) понижение частот излучения, объясняемое как динамическое удаление этих источников друг от друга и, в частности, от нашей Галактики, то есть как нестационарность (расширение) Метагалактики. Круговое движение является ускоренным, даже если происходит с постоянной угловой скоростью, потому что вектор скорости объекта постоянно меняет направление. Такое изменение направления скорости вызывает ускорение движущегося объекта центростремительной силой, которая толкает движущийся объект по направлению к центру круговой орбиты. Без этого ускорения объект будет двигаться прямолинейно в соответствии с законами Ньютона. Синхро́нная орби́та — такая орбита, на которой период обращения спутника равен периоду осевого вращения центрального тела. Гиперболи́ческая траекто́рия — в астродинамике и небесной механике траектория объекта вокруг центрального тела со скоростью, достаточной для преодоления притяжения центрального тела. Форма траектории в нерелятивистском случае является гиперболой. Эксцентриситет орбиты превышает единицу. Нитяно́й микро́метр — вспомогательное устройство к микроскопам, телескопам, геодезическим и иным оптическим инструментам, позволяющее выполнять точные измерения малых линейных или угловых расстояний. Сверхмасси́вная чёрная дыра́ — это чёрная дыра с массой 105—1010 масс Солнца. По состоянию на 2014 год сверхмассивные чёрные дыры обнаружены в центре многих галактик, включая Млечный Путь. Оптический телескоп — телескоп, собирающий и фокусирующий электромагнитное излучение оптического диапазона. Его основные задачи увеличить блеск и видимый угловой размер объекта, то есть, увеличить количество света, приходящего от небесного тела (оптическое проницание) и дать возможность изучить мелкие детали наблюдаемого объекта (разрешающая способность). Увеличенное изображение изучаемого объекта наблюдается глазом или фотографируется. Основные параметры, которые определяют характеристики телескопа… В математике и физике барице́нтр, или геометри́ческий центр, двумерной области — это среднее арифметическое положений всех точек фигуры. Определение распространяется на любой объект в n-мерном пространстве — барицентр является средним положением всех точек фигуры по всем координатным направлениям. Неформально — это точка равновесия фигуры, вырезанной из картона в предположении, что картон имеет постоянную плотность и гравитационное поле постоянно по величине и направлению.

Подробнее: Барицентр

Спагеттификация (англ. Spaghettification) — астрофизический термин (иногда также называемый эффектом лапши) для обозначения сильного растяжения объектов по вертикали и горизонтали (то есть уподобления их виду спагетти), вызванного большой приливной силой в очень сильном неоднородном гравитационном поле. В предельных случаях, когда объекты находятся возле чёрных дыр, деформация при подобном растяжении настолько сильна, что никакой объект не может сохранить свою структуру. Функция масс двойных звёзд (англ. Binary mass function) — функция, создающая ограничения для массы ненаблюдаемого компонента (звезды или экзопланеты) в спектрально-двойных звёздах или планетных системах с одной линией. Значение определяется по наблюдаемым характеристикам: по орбитальному периоду двойной системы и пику лучевой скорости наблюдаемой звезды. Скорость одного компонента двойной и орбитальный период двойной системы предоставляют частичную информацию о расстоянии и гравитационном взаимодействии… Асфери́ческими называют линзы, одна или обе поверхности которых не являются сферическими.

Подробнее: Асферическая линза

Видимая звёздная величина (m) — мера яркости небесного тела (точнее, освещённости, создаваемой этим телом) с точки зрения земного наблюдателя. Обычно используют величину, скорректированную до значения, которое она имела бы при отсутствии атмосферы. Чем ярче объект, тем меньше его звёздная величина. Тела вращения — объёмные тела, возникающие при вращении плоской геометрической фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости. Кривая блеска — функция изменения блеска астрономического объекта во времени. Данное понятие применимо как к самосветящимся объектам (звёздам), так и к объектам, отражающим свет близлежащего светила (Солнца, звезды). В роли таких объектов могут выступать планеты, их спутники, астероиды и др. Альбе́до (от лат. albus «белый») — характеристика диффузной отражательной способности поверхности. Афока́льная опти́ческая систе́ма, телескопи́ческая опти́ческая систе́ма — оптическая система (фокусное расстояние которой неограниченно большое), преобразующая параллельный световой пучок в параллельный же, но с другим углом наклона оптической оси. Предназначена главным образом для наблюдения удалённых объектов. Углова́я ско́рость — величина, характеризующая скорость вращения материальной точки вокруг центра вращения. Для вращения в двухмерном пространстве угловая скорость выражается числом, в трёхмерном пространстве представляется псевдовектором (аксиальным вектором), а в общем случае — кососимметрическим тензором. Внешний вид объектов, двигающихся с релятивистской скоростью, существенно зависит от формы объекта и способа его наблюдения. Можно выделить два основных способа: одновременное фиксирование положения точек поверхности и фотографирование при помощи ортогонального или проективного отображения. Вращение звезды — это вращательное движение звезды вокруг своей оси. Скорость вращения может быть измерена по смещению линий в её спектре или по времени движения активных элементов («звёздных пятен») на поверхности. Вращение звезды создаёт экваториальную выпуклость за счёт центробежных сил. Так как звёзды не являются твёрдыми телами, у них также может существовать дифференциальное вращение; другими словами, экватор звезды может вращаться с другой угловой скоростью, чем области в высоких широтах… Эллипсоидальные переменные (Вращающиеся эллипсоидальные переменные, Ell) — класс переменных тесных двойных, в котором звёзды так близки, хотя не обязательно в контакте, что одна или обе имеют форму эллипсоида. Причиной подобной формы является быстрое вращение и/или гравитационное взаимодействие звёзд. Их видимый суммарный блеск меняется с периодом, равным периоду орбитального обращения, вследствие изменения площади излучающей поверхности, обращенной к наблюдателю.

Подробнее: Эллипсоидальная переменная

Суперъяйцо́ — в геометрии тело вращения, полученное путём вращения суперэллипса с показателем степени больше 2 вокруг его длинной оси. Является частным случаем суперэллипсоида. Средняя долгота (англ. Mean longitude) — эклиптическая долгота, на которой бы находилось обращающееся тело, если бы оно двигалось по невозмущённой круговой орбите. На практике представляет собой гибридный угол. Ра́диус (лат. radius — спица колеса, луч) — отрезок, соединяющий центр окружности (или сферы) с любой точкой, лежащей на окружности (или сфере), а также длина этого отрезка. Радиус составляет половину диаметра. Фокус — в геометрии точка, относительно которой (которых) проводится построение некоторых кривых. Например, один или два фокуса могут использоваться при построении конических сечений, в число которых входит окружность, эллипс, парабола и гипербола. Также два фокуса используются при построении овала Кассини и овала Декарта. Большее число фокусов рассматривается при определении n-эллипса. Ко́матическая аберрация или Ко́ма (от др.-греч. κόμη — волосы) — одна из пяти аберраций Зейделя оптических систем, приводящая к нарушению гомоцентричности широких световых пучков, входящих в систему под углом к оптической оси.