Перестановка — Википедия
 6 перестановок трёх шаров
6 перестановок трёх шаровВ комбинаторике перестано́вка — это упорядоченный набор без повторений чисел 1,2,…,n,{\displaystyle 1,2,\ldots ,n,} обычно трактуемый как биекция на множестве {1,2,…,n}{\displaystyle \{1,2,\ldots ,n\}}, которая числу i ставит в соответствие i-й элемент из набора. Число n при этом называется длиной перестановки[1].
В теории групп под перестановкой произвольного множества подразумевается биекция этого множества на себя. Как синоним слову «перестановка» в этом смысле некоторые авторы используют слово подстановка. (Другие авторы подстановкой называют наглядный способ записи перестановки.)
Термин перестановка возник потому, что сначала брались объекты, каким-то образом расставленные, а другие способы упорядочения требовали переставить эти объекты.
- Pn=Ann=n!(n−n)!=n!0!=n!=1⋅2⋅⋯⋅n.{\displaystyle P_{n}=A_{n}^{n}={\frac {n!}{(n-n)!}}={\frac {n!}{0!}}=n!=1\cdot 2\cdot \dots \cdot n.}
Специальные типы перестановок[править | править код]
- Тождественная перестановка — перестановка e,{\displaystyle e,} которая каждый элемент x∈X{\displaystyle x\in X} отображает в себя: e(x)=x.{\displaystyle e(x)=x.}
- Инволюция — перестановка τ,{\displaystyle \tau ,} которая является обратной самой себе, то есть τ⋅τ=e.{\displaystyle \tau \cdot \tau =e.}
- Беспорядок — перестановка без неподвижных точек.
- Циклом длины ℓ{\displaystyle \ell } называется такая подстановка π,{\displaystyle \pi ,} которая тождественна на всём множестве X,{\displaystyle X,} кроме подмножества {x1,x2,…,xℓ}⊂X{\displaystyle \{x_{1},x_{2},\dots ,x_{\ell }\}\subset X} и π(xℓ)=x1,π(xi)=xi+1.{\displaystyle \pi (x_{\ell })=x_{1},\pi (x_{i})=x_{i+1}.} Обозначается (x1,x2,…,xℓ).{\displaystyle (x_{1},x_{2},\dots ,x_{\ell }).}.
- Транспозиция — перестановка элементов множества X{\displaystyle X}, которая меняет местами два элемента. Транспозиция является циклом длины 2.
Подстановка[править | править код]
Перестановка π{\displaystyle \pi } множества X{\displaystyle X} может быть записана в виде подстановки, например:
- (x1x2x3…xny1y2y3…yn),{\displaystyle {\begin{pmatrix}x_{1}&x_{2}&x_{3}&\dots &x_{n}\\y_{1}&y_{2}&y_{3}&\dots &y_{n}\end{pmatrix}},}
где {x1,…,xn}={y1,…,yn}=X{\displaystyle \{x_{1},\dots ,x_{n}\}=\{y_{1},\dots ,y_{n}\}=X} и π(xi)=yi.{\displaystyle \pi (x_{i})=y_{i}.}
Произведения циклов и знак перестановки[править | править код]
Любая перестановка π{\displaystyle \pi } может быть разложена в произведение (композицию) непересекающихся циклов длины ℓ⩾2{\displaystyle \ell \geqslant 2}, причём единственным образом с точностью до порядка следования циклов в произведении. Например:
- (123456516423)=(1,5,2)(3,6).{\displaystyle {\begin{pmatrix}1&2&3&4&5&6\\5&1&6&4&2&3\end{pmatrix}}=(1,5,2)(3,6).}
Часто также считают, что неподвижные точки перестановки представляют собой самостоятельные циклы длины 1, и дополняют ими цикловое разложение перестановки. Для приведенного выше примера таким дополненным разложением будет (1,5,2)(3,6)(4){\displaystyle (1,5,2)(3,6)(4)}. Количество циклов разной длины, а именно набор чисел (c1,c2,…){\displaystyle (c_{1},c_{2},\dots )}, где cℓ{\displaystyle c_{\ell }} — это количество циклов длины ℓ{\displaystyle \ell }, определяет цикловую структуру перестановки. При этом величина 1⋅c1+2⋅c2+…{\displaystyle 1\cdot c_{1}+2\cdot c_{2}+\dots } равна длине перестановки, а величина c1+c2+…{\displaystyle c_{1}+c_{2}+\dots } равна общему количеству циклов. Количество перестановок из n элементов с k циклами даётся числом Стирлинга первого рода без знака [nk]{\displaystyle {\begin{bmatrix}n\\k\end{bmatrix}}}.
Любой цикл может быть разложен в произведение (не обязательно непересекающихся) транспозиций. При этом цикл длины 1 (являющийся по сути тождественной перестановкой
- (x1,…,xl)=(x1,xℓ)(x1,xℓ−1)…(x1,x2).{\displaystyle (x_{1},\dots ,x_{l})=(x_{1},x_{\ell })(x_{1},x_{\ell -1})\dots (x_{1},x_{2}).}
Следует заметить, что разложение циклов на произведение транспозиций не является единственным:
- (1,2,3)=(1,3)(1,2)=(2,3)(1,3)=(1,3)(2,4)(2,4)(1,2).{\displaystyle (1,2,3)=(1,3)(1,2)=(2,3)(1,3)=(1,3)(2,4)(2,4)(1,2).}
Таким образом, любая перестановка может быть разложена в произведение транспозиций. Хотя это можно сделать многими способами, чётность количества транспозиций во всех таких разложениях одинакова. Это позволяет определить знак перестановки (чётностью перестановки
или сигнатурой перестановки) π{\displaystyle \pi } как- επ=(−1)t,{\displaystyle \varepsilon _{\pi }=(-1)^{t},}
где t{\displaystyle t} — количество транспозиций в каком-то разложении π{\displaystyle \pi }. При этом π{\displaystyle \pi } называют чётной перестановкой, если επ=1,{\displaystyle \varepsilon _{\pi }=1,} и нечётной перестановкой, если επ=−1.{\displaystyle \varepsilon _{\pi }=-1.}
Эквивалентно, знак перестановки определяется её цикловой структурой: знак перестановки π{\displaystyle \pi } из n{\displaystyle n} элементов, состоящий из k{\displaystyle k} циклов, равен
- επ=(−1)n−k.{\displaystyle \varepsilon _{\pi }=(-1)^{n-k}.}
Знак перестановки π{\displaystyle \pi } также может быть определен через количество инверсий N(π){\displaystyle N(\pi )} в π{\displaystyle \pi }:
- επ=(−1)N(π).{\displaystyle \varepsilon _{\pi }=(-1)^{N(\pi )}.}
Рассмотрим n элементов m различных типов, причем в каждом типе все элементы одинаковы. Тогда перестановки из всех этих элементов с точностью до порядка следования однотипных элементов называются перестановками с повторением. Если ki — количество элементов i-го типа, то k1+k2+⋯+km=n{\displaystyle k_{1}+k_{2}+\dots +k_{m}=n} и количество всевозможных перестановок с повторениями равно мультиномиальному коэффициенту (nk1, k2, …, km)=n!k1!k2!…km!.{\displaystyle \textstyle {\binom {n}{k_{1},\ k_{2},\ \dots ,\ k_{m}}}={\frac {n!}{k_{1}!k_{2}!\dots k_{m}!}}.}
Перестановку с повторениями можно также рассматривать как перестановку мультимножества {1k1,2k2,…,mkm}{\displaystyle \{1^{k_{1}},2^{k_{2}},\dots ,m^{k_{m}}\}} мощности k1+k2+⋯+km=n{\displaystyle k_{1}+k_{2}+\dots +k_{m}=n}.
Случайной перестановкой называется случайный вектор ξ=(ξ1,…,ξn),{\displaystyle \xi =(\xi _{1},\ldots ,\xi _{n}),} все элементы которого принимают натуральные значения от 1 до n,{\displaystyle n,} и при этом вероятность совпадения любых двух элементов равна 0.
Независимой случайной перестановкой называется такая случайная перестановка ξ{\displaystyle \xi }, для которой
- P{ξ=σ}=p1σ(1)…pnσ(n)∑π∈Snp1π(1)…pnπ(n){\displaystyle P\{\xi =\sigma \}={\frac {p_{1\sigma (1)}\ldots p_{n\sigma (n)}}{\sum \limits _{\pi \in S_{n}}p_{1\pi (1)}\ldots p_{n\pi (n)}}}}
для некоторых pij,{\displaystyle p_{ij},} таких, что
- ∀i(1⩽i⩽n):pi1+…+pin=1{\displaystyle \forall i(1\leqslant i\leqslant n):p_{i1}+\ldots +p_{in}=1}
- ∑π∈Snp1π(1)…pnπ(n)>0.{\displaystyle \sum \limits _{\pi \in S_{n}}p_{1\pi (1)}\ldots p_{n\pi (n)}>0.}
Если при этом pij{\displaystyle p_{ij}} не зависят от i{\displaystyle i}, то перестановку ξ{\displaystyle \xi } называют одинаково распределённой. Если же нет зависимости от j{\displaystyle j}, то есть ∀i,j(1≤i,j≤n):pij=1/n,{\displaystyle \scriptstyle \forall i,j(1\leq i,j\leq n):p_{ij}=1/n,} то ξ{\displaystyle \xi } называют однородной.
Лекция 20. Перестановки. Определитель
5
Лекции по алгебре и геометрии. Семестр 2.
Лекция 20. Перестановки. Определение определителя.
Краткое содержание: перестановки конечного множества, их количество, инверсии, четность перестановки, транспозиция и ее свойства, определитель, член определителя и его знак. Свойства определителя.
Глава 2. Определение определителя n-го порядка.
п.1. Перестановки.
Пусть М – множество
из 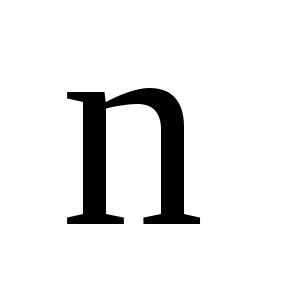 элементов:
элементов: 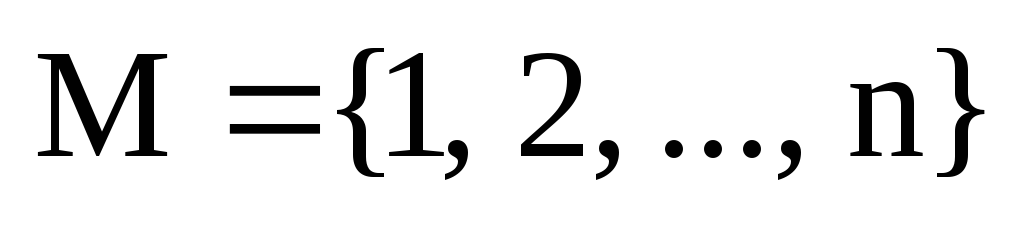 .
.
Определение. Перестановкой множества из n элементов называется любой упорядоченный набор из всех элементов этого множества, среди которых нет одинаковых.
Пример. Упорядоченные наборы:
(1, 2, 3, 4, 5), (5, 2, 1, 4, 3), (2, 5, 4, 1, 3)
являются перестановками множества M, а наборы
(3, 2, 1, 5), (3, 2, 1, 4, 3), (3, 2, 6, 4, 5)
не являются перестановками множества М.
Определение.
Перестановку 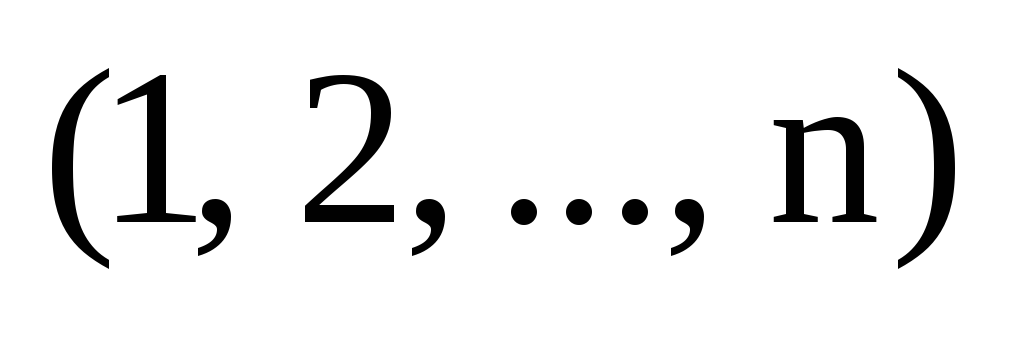 множества М называют начальной
перестановкой.
множества М называют начальной
перестановкой.
Теорема. (О количестве перестановок.)
Существует ровно  перестановок множества из
перестановок множества из 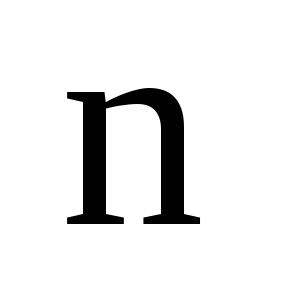 элементов.
элементов.
Доказательство. Доказательство проводится методом математической индукции.
1) База индукции.
Пусть 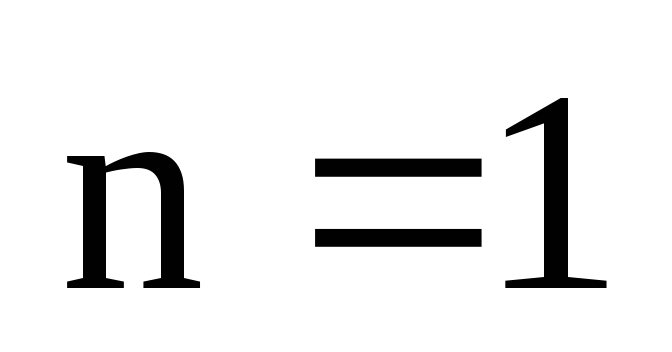 ,
т.е.
,
т.е. 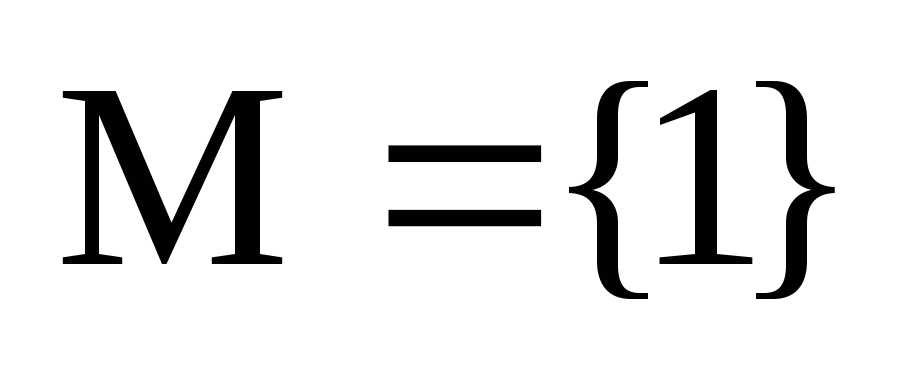 .
Очевидно, что существует единственная
перестановка множества из одного
элемента: (1).
.
Очевидно, что существует единственная
перестановка множества из одного
элемента: (1).
2) Индукционная гипотеза.
Пусть существует
ровно  перестановок множества из
перестановок множества из 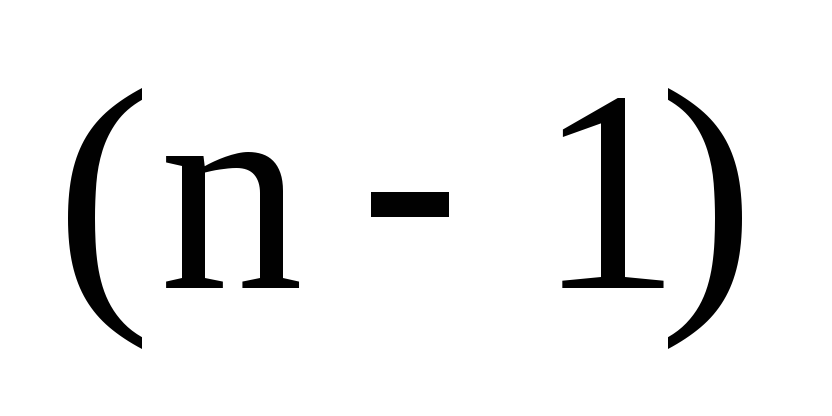 -го
элемента:
-го
элемента:  .
Добавим к каждой перестановке множества
А еще один элемент: n. Этот
элемент можно поставить на 1-е место или
2-е или … или n-е место.
Добавляя к каждой перестановке множества
А элемент n на k-е
место мы получаем, в соответствии с
индукционным предположением,
.
Добавим к каждой перестановке множества
А еще один элемент: n. Этот
элемент можно поставить на 1-е место или
2-е или … или n-е место.
Добавляя к каждой перестановке множества
А элемент n на k-е
место мы получаем, в соответствии с
индукционным предположением, 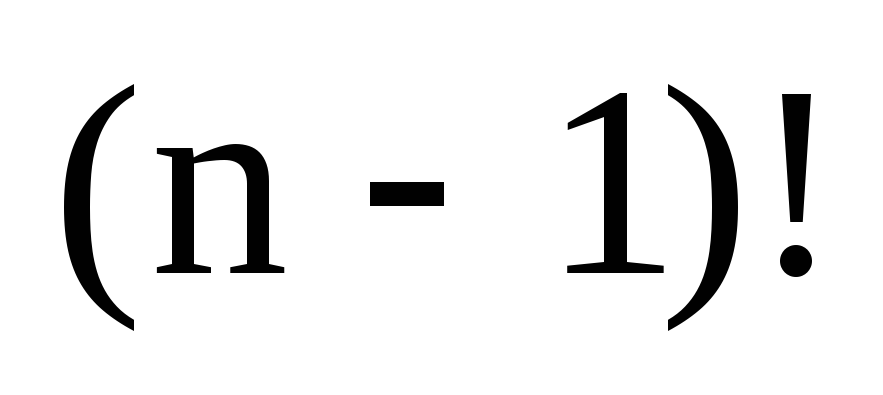 перестановок уже множества М. Проделав
это n раз при
перестановок уже множества М. Проделав
это n раз при 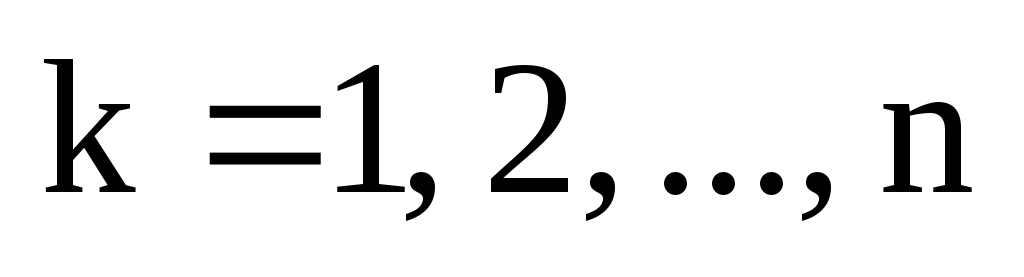 мы получим всего
мы получим всего  перестановок множества М, ч.т.д.
перестановок множества М, ч.т.д.
Теорема доказана.
Определение.
Говорят, что пара чисел (i,
j) образуют в перестановке
инверсию, если 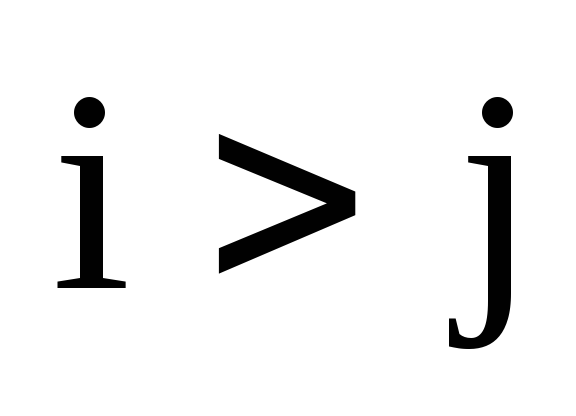 ,
но число i находится в
перестановке левее числа j.
,
но число i находится в
перестановке левее числа j.
Пример. В перестановке (2, 5, 4, 1, 3) инверсию образуют пары чисел (2, 1), (5, 4), (5, 1), (5, 3), (4, 1) и (4, 3).
Обозначения:
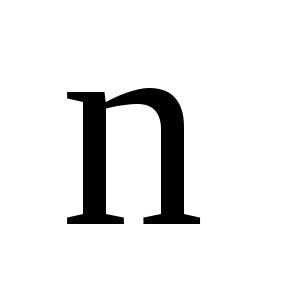 элементов обозначают так:
элементов обозначают так: 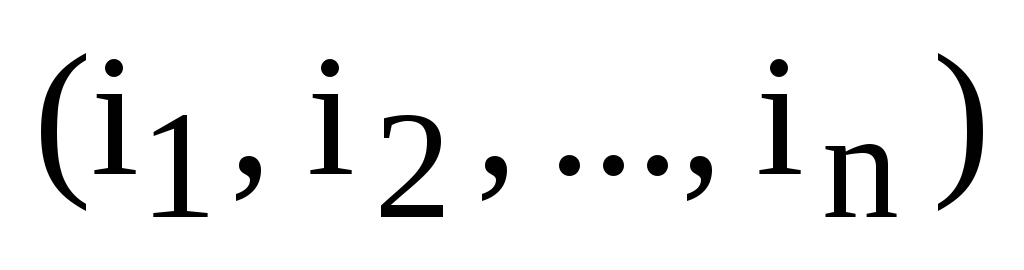 .
Здесь каждое число перестановки
обозначают буквой с нижним индексом.
Индекс показывает, в каком месте
перестановки стоит данное число.
Например, число
.
Здесь каждое число перестановки
обозначают буквой с нижним индексом.
Индекс показывает, в каком месте
перестановки стоит данное число.
Например, число 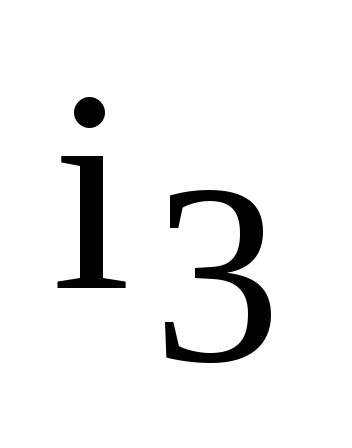 ,
стоит в перестановке третьим по счету.
,
стоит в перестановке третьим по счету. Число (количество)
всех инверсий в перестановке 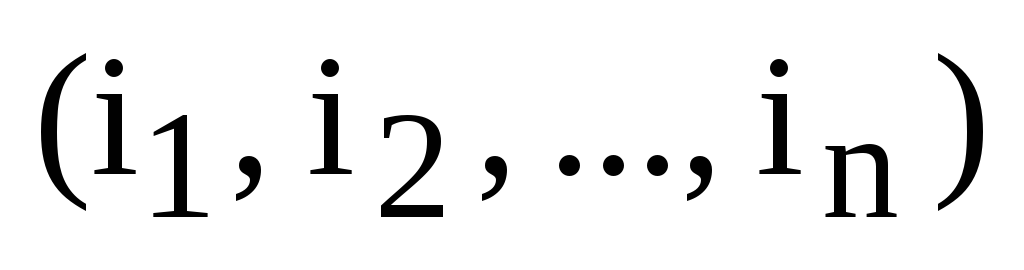 мы будем обозначать
мы будем обозначать 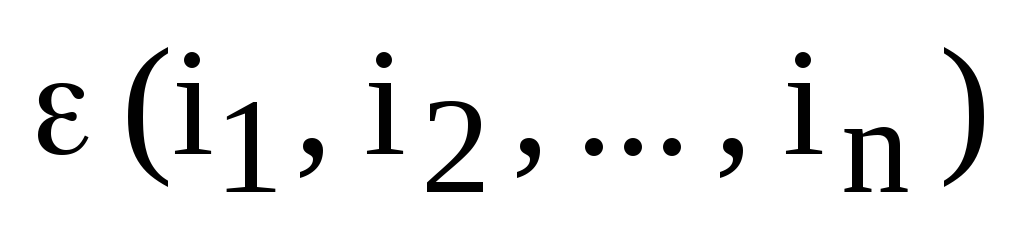 .
Так, например,
.
Так, например, 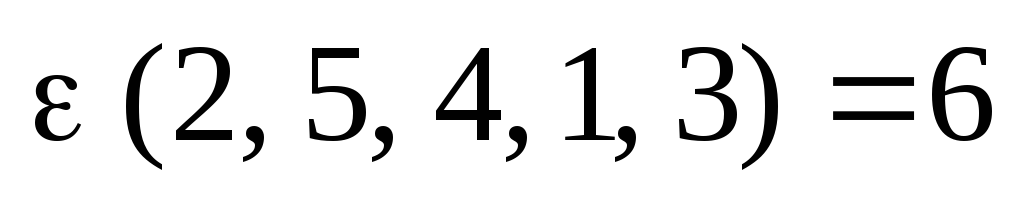 .
.
Определение. Перестановка называется четной, если число ее инверсий четно, и нечетной в противном случае.
Пример. Перестановка
(2, 5, 4, 1, 3) четная, т.к. 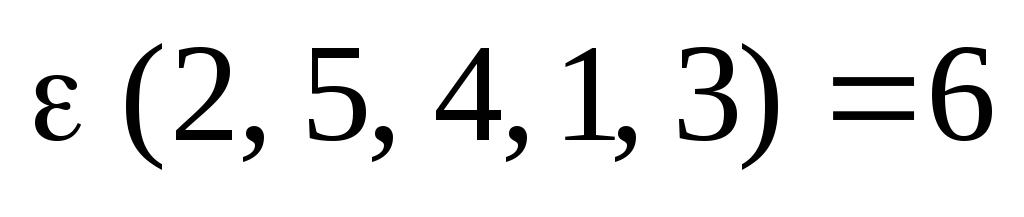 – четное число, а перестановка
– четное число, а перестановка 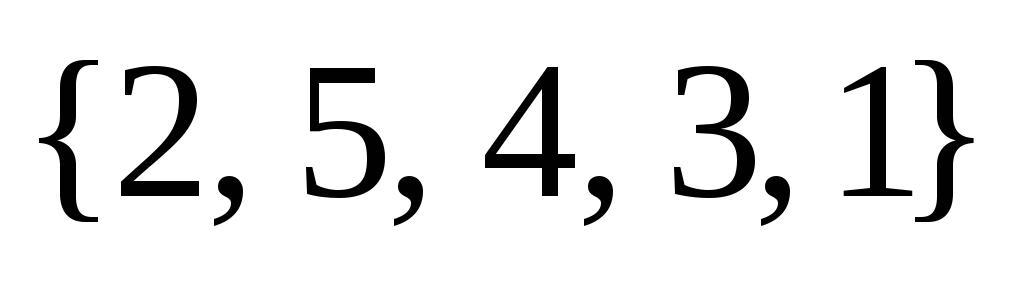 – нечетная, т.к.
– нечетная, т.к. 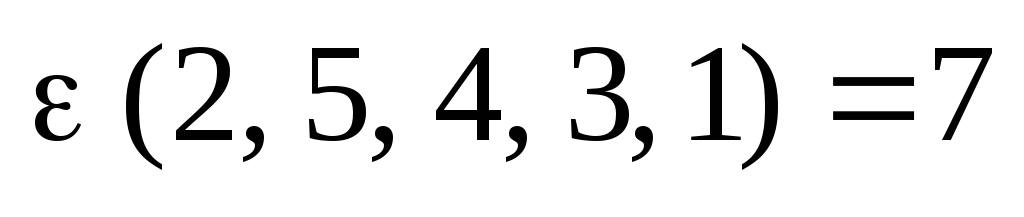 .
.
Определение. Транспозицией называется действие, заключающееся в том, что в перестановке два каких-либо числа меняют местами друг с другом.
Обозначение: 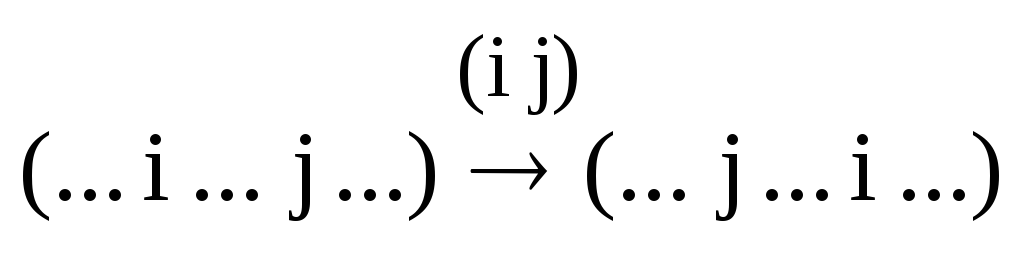
Пример. 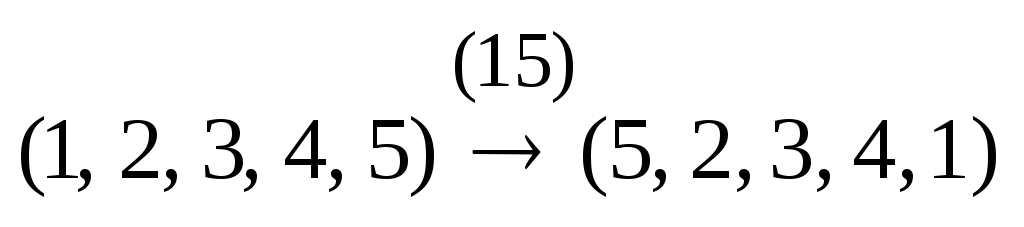 .
.
Теорема. Любая транспозиция соседних элементов перестановки меняет четность перестановки на противоположную.
Доказательство.
Пусть дана перестановка 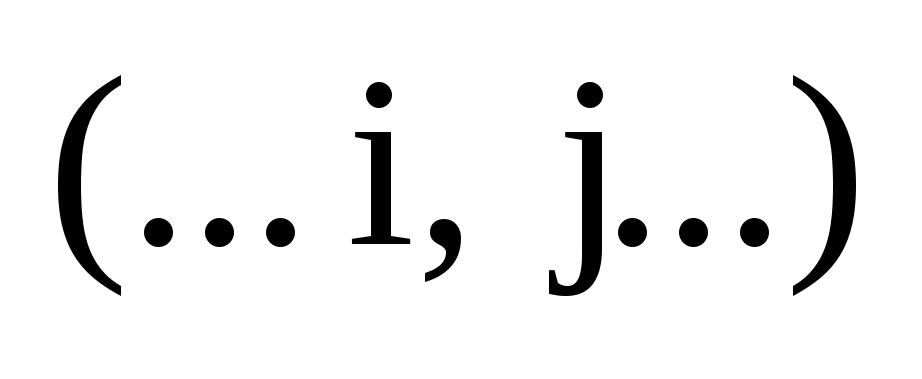
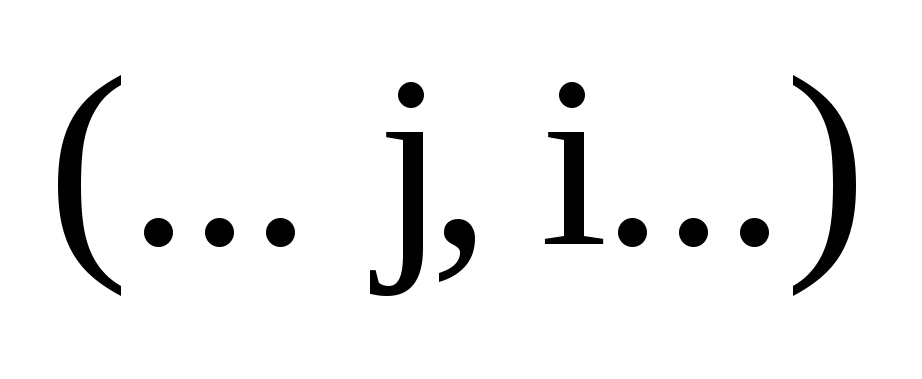 .
Сразу заметим, что все пары, которые
образовывали инверсию в старой
перестановке, образуют инверсию и в
новой, кроме возможно одной пары: (i,
j). Если эта пара давала
инверсию в старой перестановке, то в
новой уже нет и число инверсий уменьшается
на 1. Если же эта пара не образовывала
инверсию в старой перестановке, то в
новой образует инверсию и число инверсий
увеличивается на 1. В любом случае, число
инверсий изменяется на 1, а следовательно,
меняется четность перестановки.
.
Сразу заметим, что все пары, которые
образовывали инверсию в старой
перестановке, образуют инверсию и в
новой, кроме возможно одной пары: (i,
j). Если эта пара давала
инверсию в старой перестановке, то в
новой уже нет и число инверсий уменьшается
на 1. Если же эта пара не образовывала
инверсию в старой перестановке, то в
новой образует инверсию и число инверсий
увеличивается на 1. В любом случае, число
инверсий изменяется на 1, а следовательно,
меняется четность перестановки.Теорема доказана.
Теорема. Любая транспозиция любых двух элементов перестановки меняет четность перестановки на противоположную.
Доказательство.
Пусть выполняется транспозицию (i
j) и пусть между элементами
i и j находится
m других элементов. Легко
видеть, что такую транспозицию можно
выполнить за 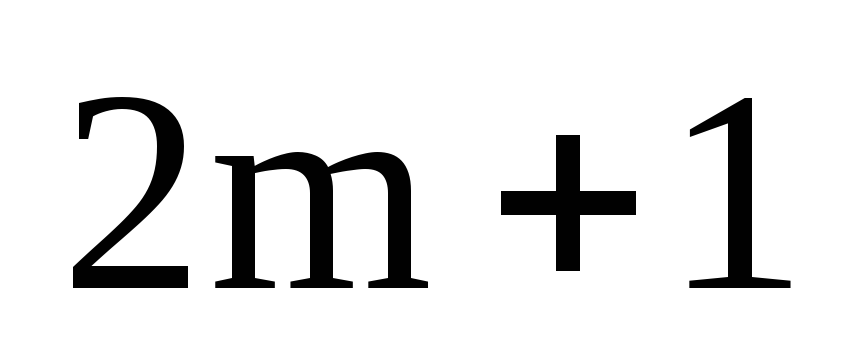
Теорема доказана.
Теорема. Любую перестановку можно получить из начальной перестановки последовательным выполнением конечного числа транспозиций, причем это количество транспозиций есть число четное, если данная перестановка четна, и нечетное в противном случае.
Доказательство. Очевидно в свете следующего примера.
Пример. 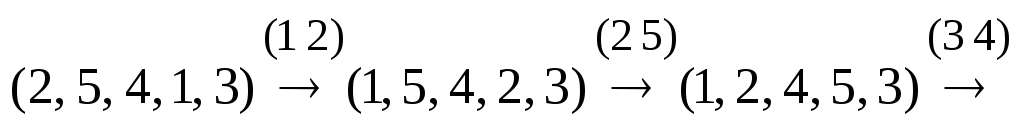
 .
.
Здесь, перестановка 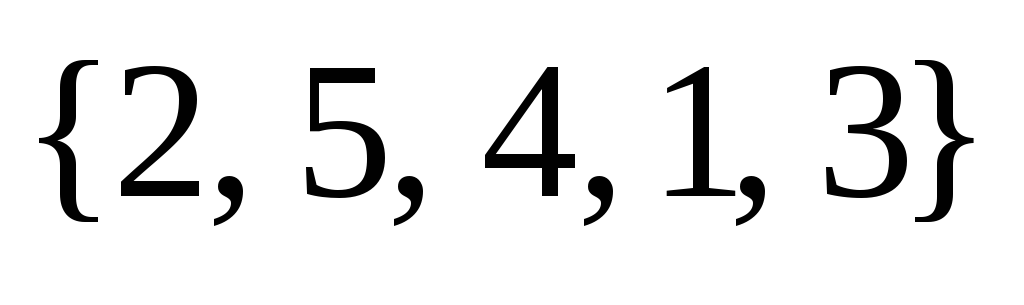 приведена к начальной за
приведена к начальной за
4 транспозиции и
она четная, т.к. 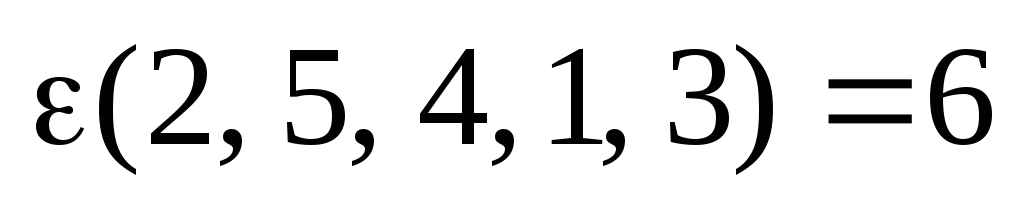 .
.
Замечание. Понятно, что любую перестановку можно привести к начальной и обратно с помощью тех же самых транспозиций, выполненных в обратном порядке.
Теорема. Количество
четных перестановок множества из 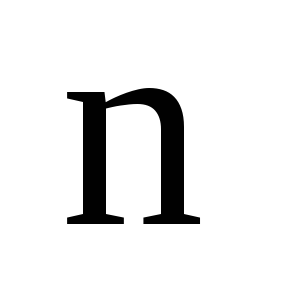 элементов равно количеству нечетных и
равно
элементов равно количеству нечетных и
равно 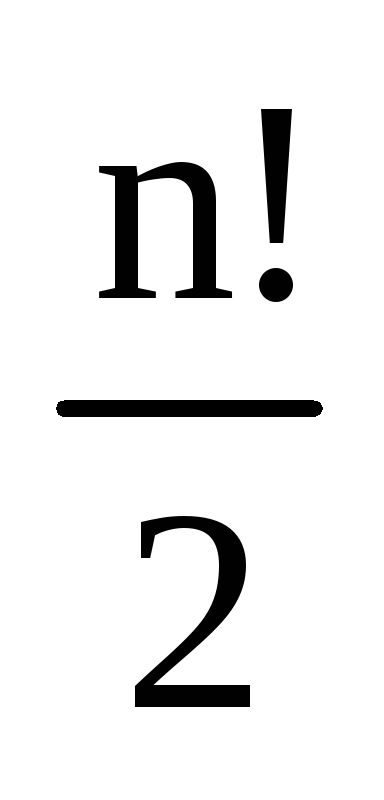 .
.
Доказательство. Каждая перестановка либо четная, либо нечетная. Поэтому общее количество четных перестановок неизменно. Так же и количество нечетных перестановок есть число фиксированное. Во всех перестановках выполним одну и ту же транспозицию, например, (1 2). Все четные перестановки станут нечетными и наоборот, все нечетные станут четными. Следовательно, четных и нечетных перестановок одинаковое количество.
Теорема доказана.
Замечание. Предлагается следующая интерпретация к предыдущей теореме.
Пусть на некоторой вечеринке находится какое-то количество людей, причем все женщины в шляпках, а мужчины в масках. Допустим, что в некоторый момент времени, каждый мужчина должен отдать женщине свою маску и получить от нее головной убор. Каково должно быть соотношение мужчин и женщин, чтобы каждый мужчина получил шляпку, а каждая женщина – маску?
Ответ очевиден.
п.2.
Определение определителя 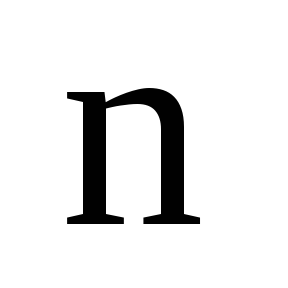 –
го порядка.
–
го порядка.
Пусть дана
квадратная матрица 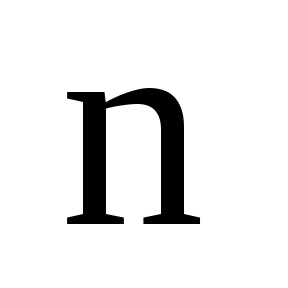 –
го порядка:
–
го порядка:
 .
.
Определение.
Произведение 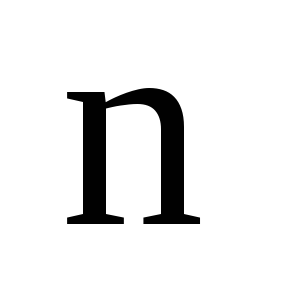 элементов матрицы А, взятых по одному
из каждой строки и каждого столбца
называют членом определителя матрицы
А.
элементов матрицы А, взятых по одному
из каждой строки и каждого столбца
называют членом определителя матрицы
А.
Обозначение: 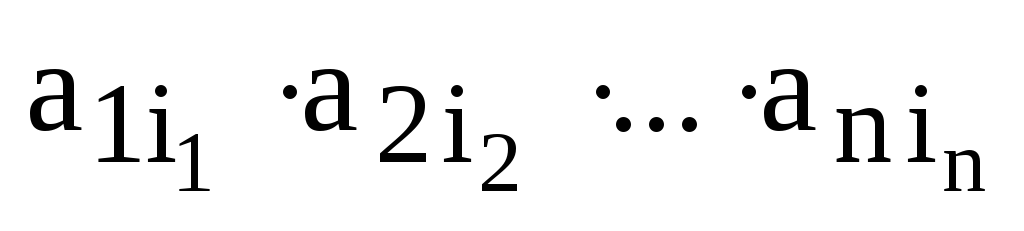 .
.
Здесь первый
индекс обозначает номер строки, из
которой взят элемент, второй индекс 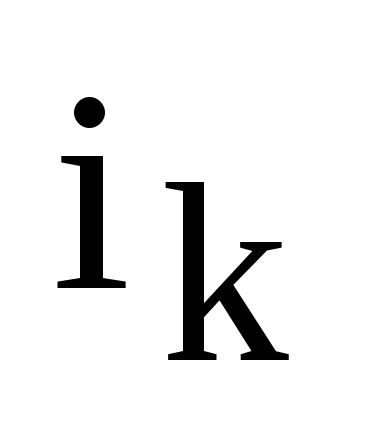 ,
он в свою очередь имеет нижний индекс
,
он в свою очередь имеет нижний индекс 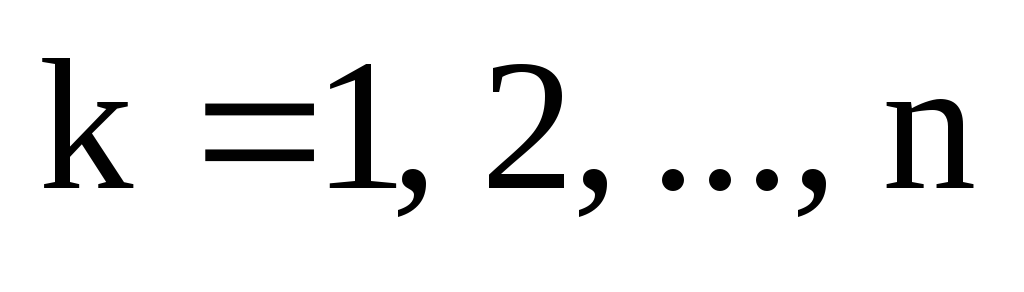 ,
обозначает номер столбца, из которой
взят элемент и набор вторых индексов
образует перестановку
,
обозначает номер столбца, из которой
взят элемент и набор вторых индексов
образует перестановку 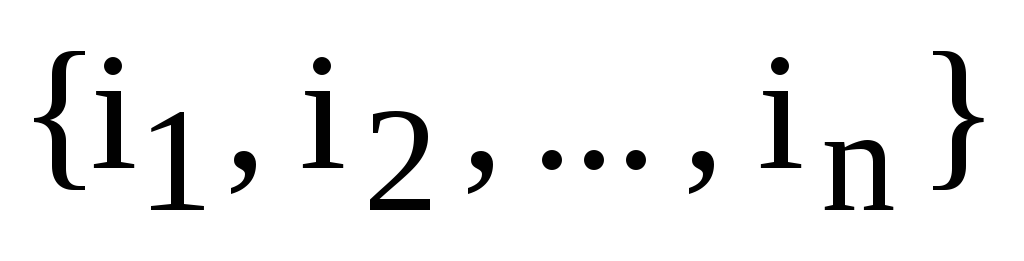 множества
множества 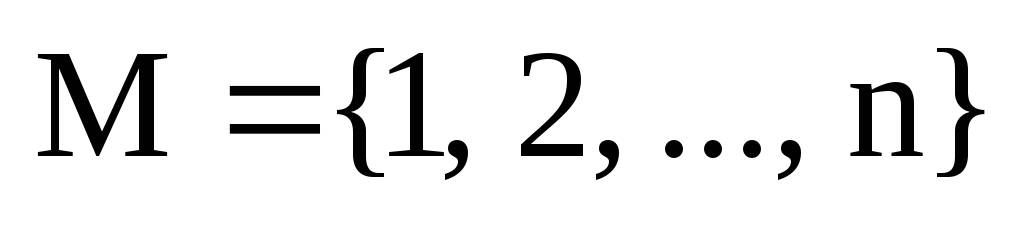 .
.
Т.к. число всех
перестановок множества 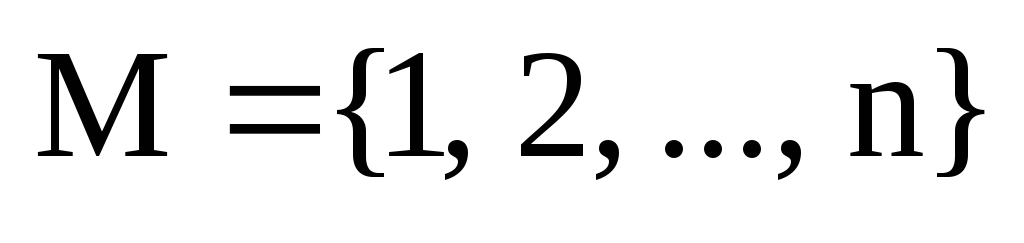 равно
равно  ,
то существует ровно
,
то существует ровно  членов определителя.
членов определителя.
Каждый член
определителя снабдим знаком плюс или
минус, в зависимости от четности или
нечетности перестановки вторых индексов.
Это можно сделать с помощью множителя 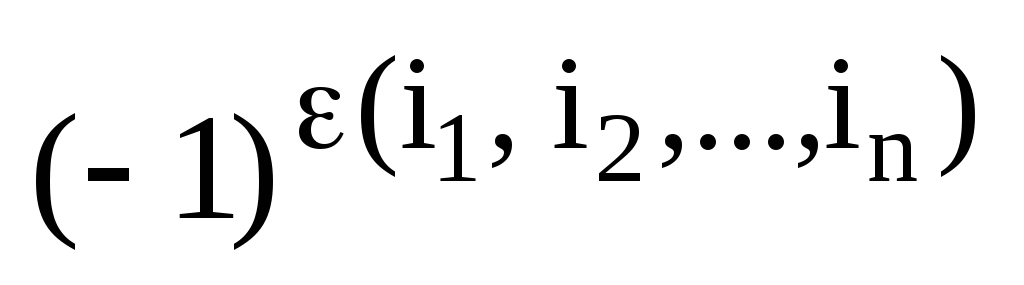 ,
который равен 1, если перестановка
,
который равен 1, если перестановка 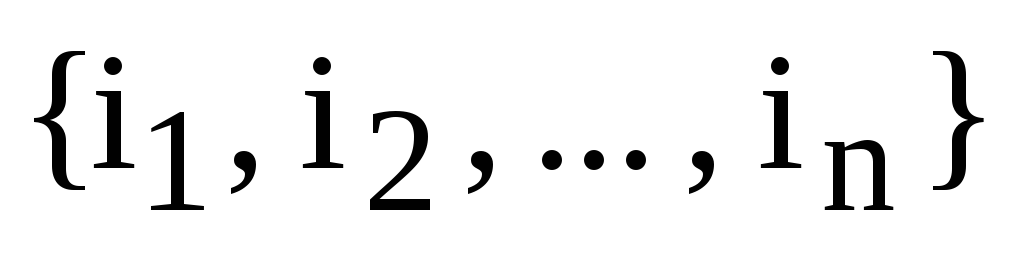 четная и тогда число инверсий
четная и тогда число инверсий 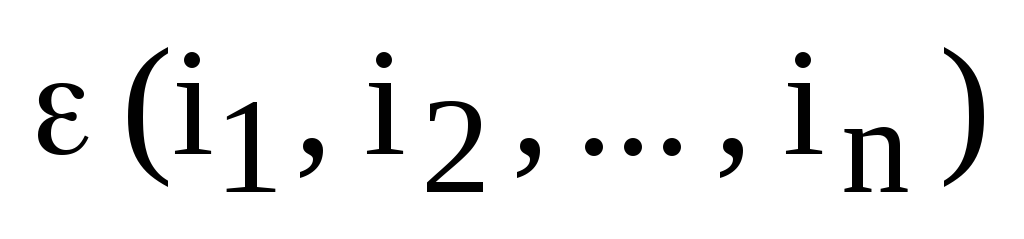 есть четное число и равен – 1, если
перестановка
есть четное число и равен – 1, если
перестановка 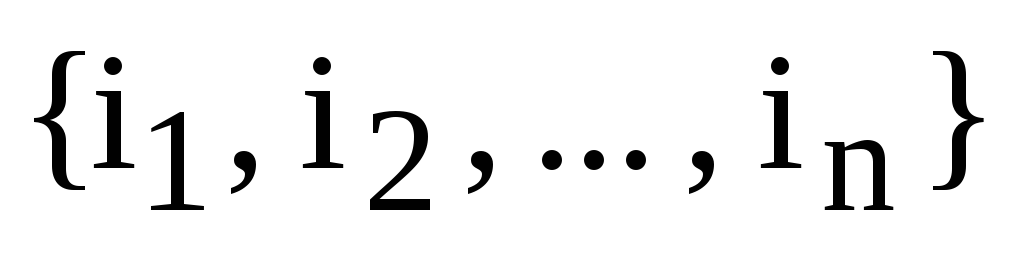 нечетная и тогда число инверсий
нечетная и тогда число инверсий 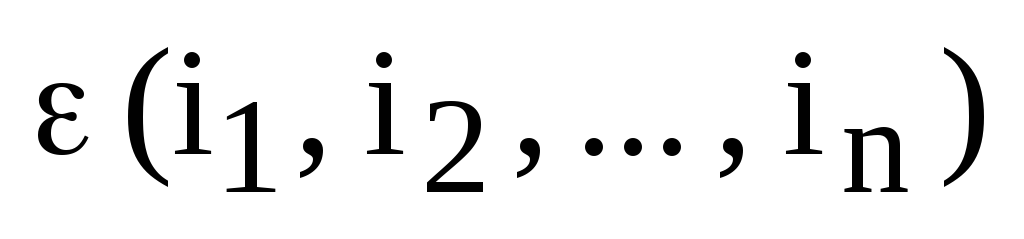 есть нечетное число.
есть нечетное число.
Определение.
Определителем (детерминантом)  –
го порядка или определителем (детерминантом)
квадратной матрицы
–
го порядка или определителем (детерминантом)
квадратной матрицы  –
го порядка называют алгебраическую
сумму всех членов определителя данной
матрицы, взятых со своими знаками.
–
го порядка называют алгебраическую
сумму всех членов определителя данной
матрицы, взятых со своими знаками.
Обозначение:

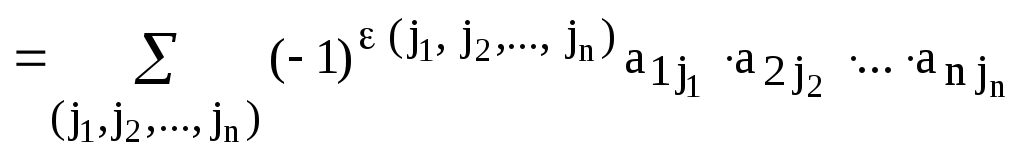 ,
(1)
,
(1)
где суммирование ведется по всем перестановкам столбцов.
Пример. Вычислим определитель 3 – го порядка:
 .
.
Выпишем все члены определителя, их ровно 6 штук. Для этого, выпишем сначала все перестановки множества из 3 элементов:
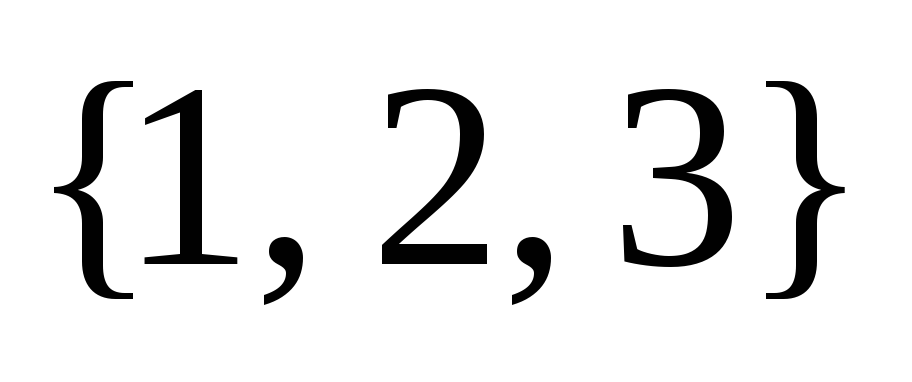 ,
, 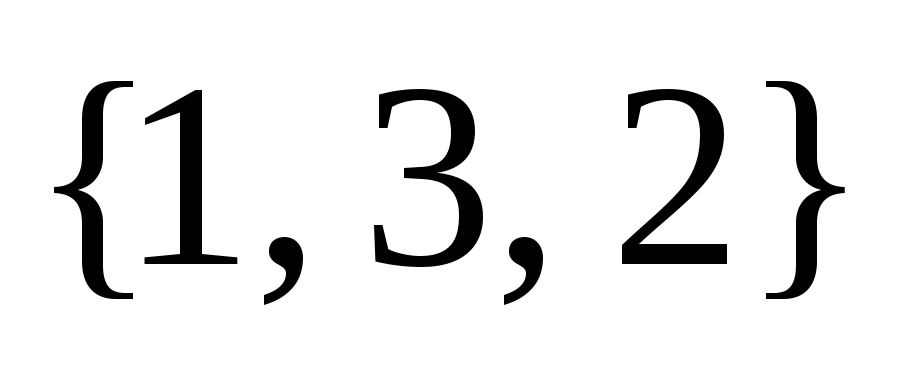 ,
, 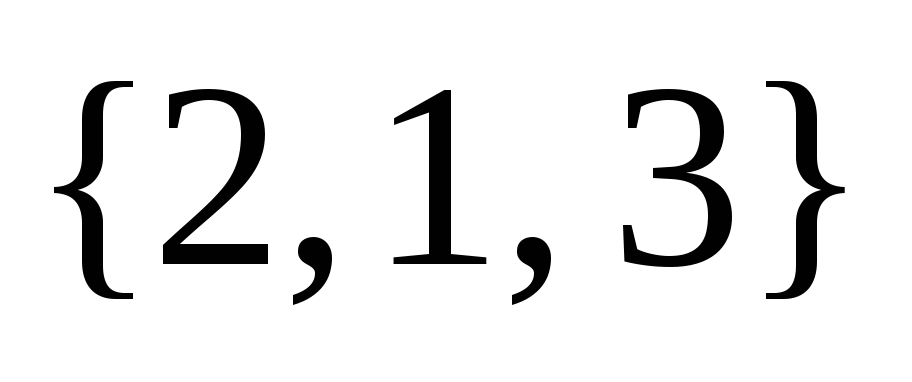 ,
, 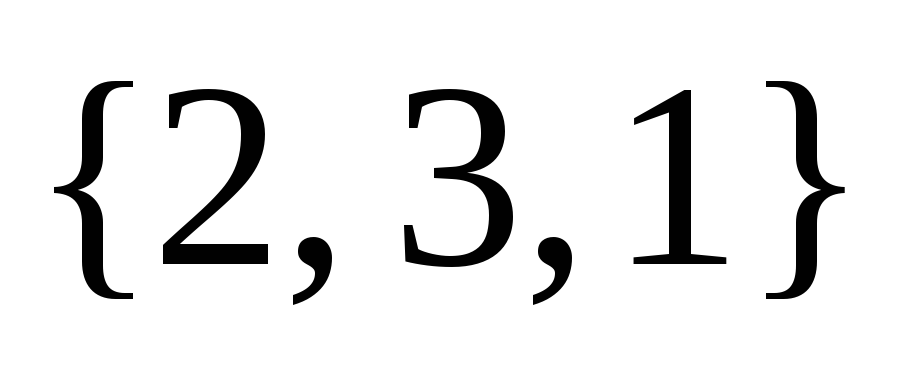 ,
, 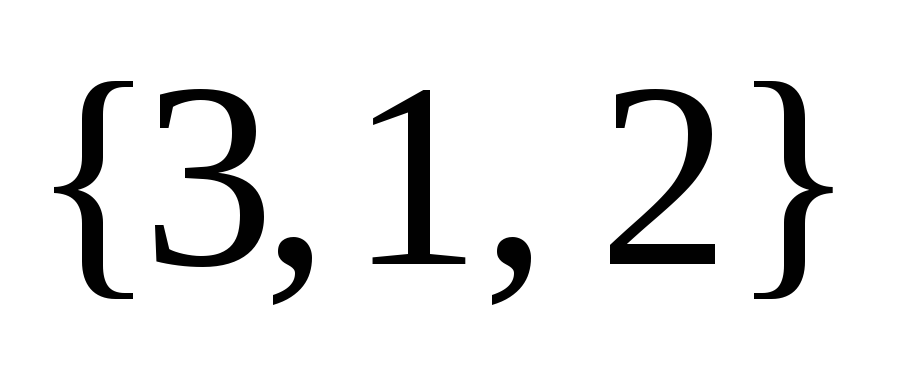 ,
, 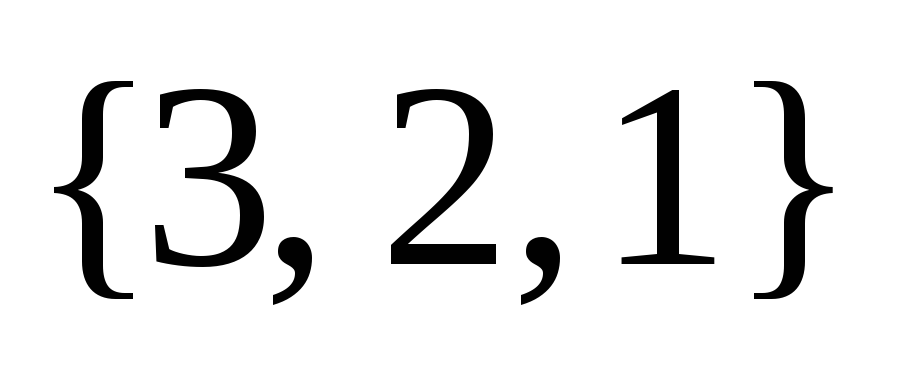 и определим их четность:
и определим их четность:
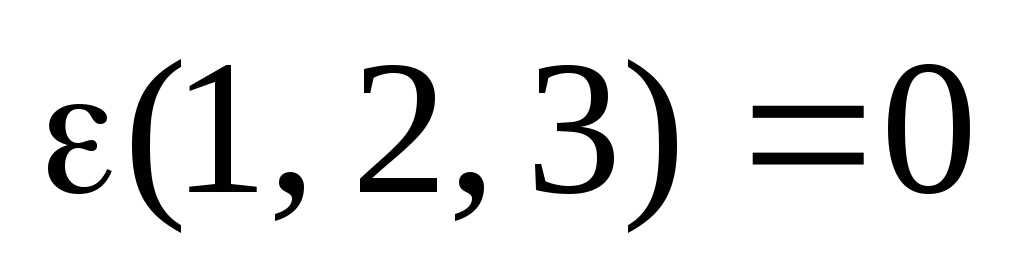 ,
, 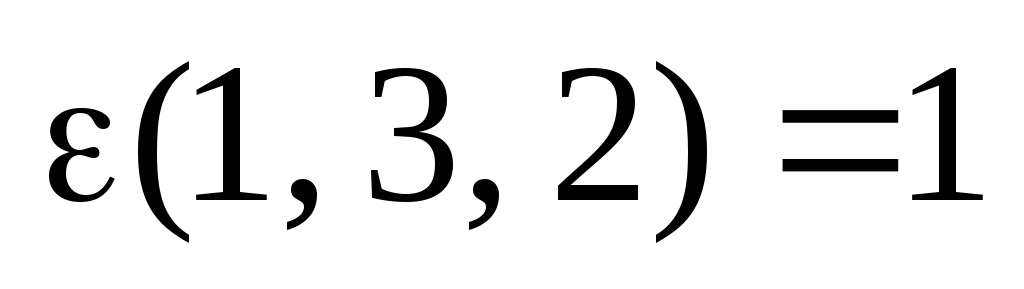 ,
, 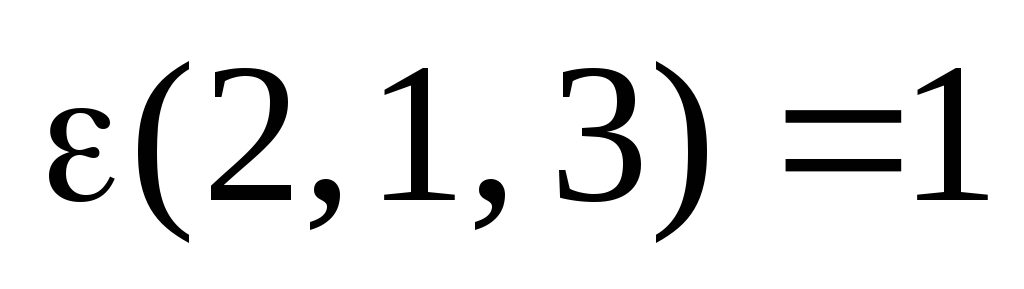 ,
, 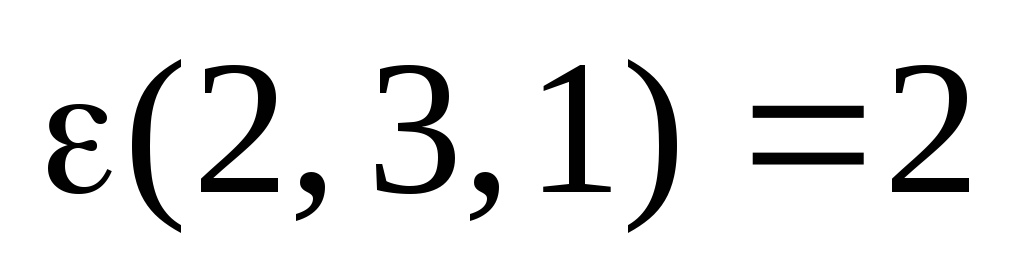 ,
, 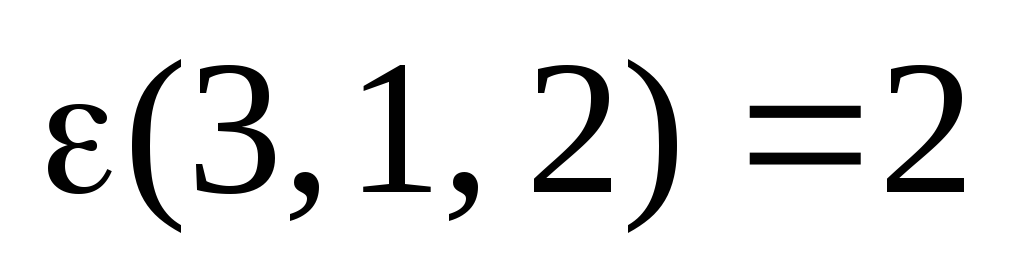 ,
,  .
.
Теперь выписываем члены определителя, причем первые индексы (номера строк) образуют начальную перестановку, а вторые индексы (номера столбцов) образуют перестановку, одну из 6 приведенных выше.
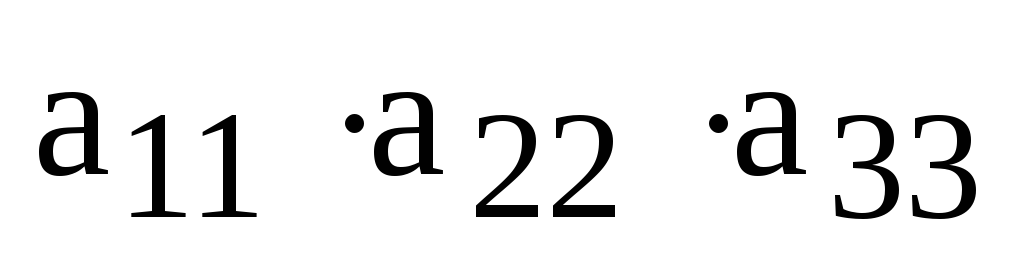 ,
, 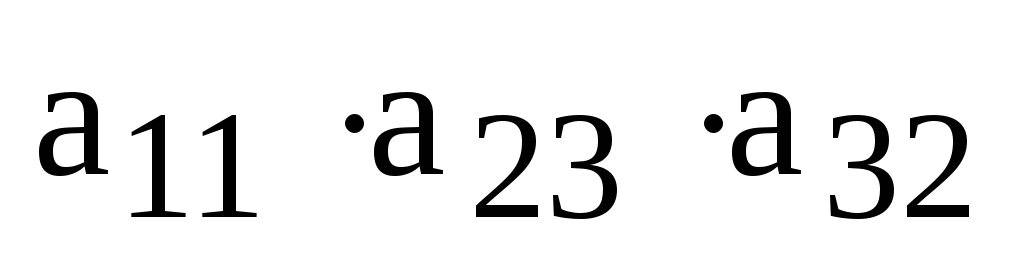 ,
, 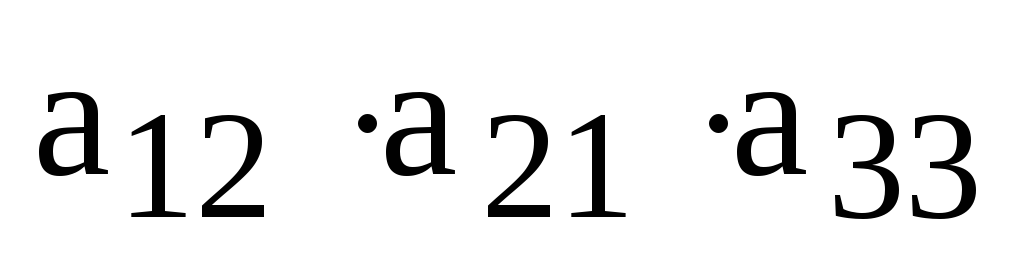 ,
, 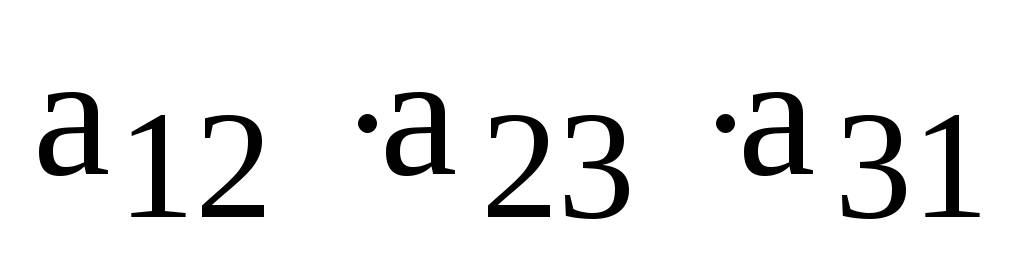 ,
, 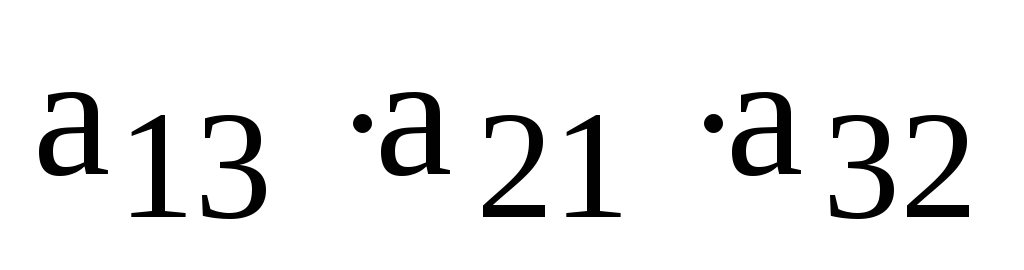 ,
, 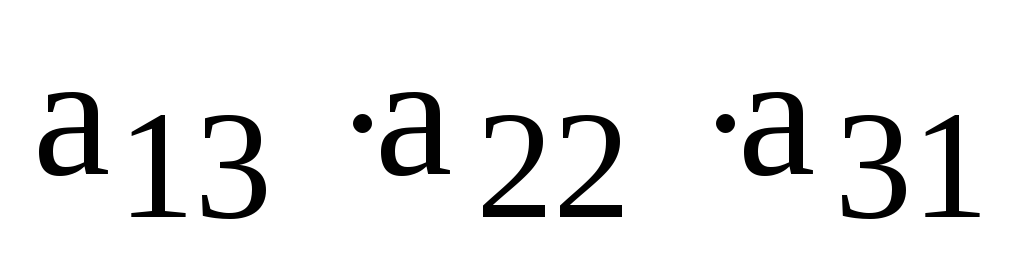 .
.
Теперь мы можем записать определитель, как
алгебраическую сумму всех членов определителей, взятых со знаком плюс, если вторые индексы сомножителей, входящих в член определителя, образуют четную перестановку, и со знаком минус в противном случае:

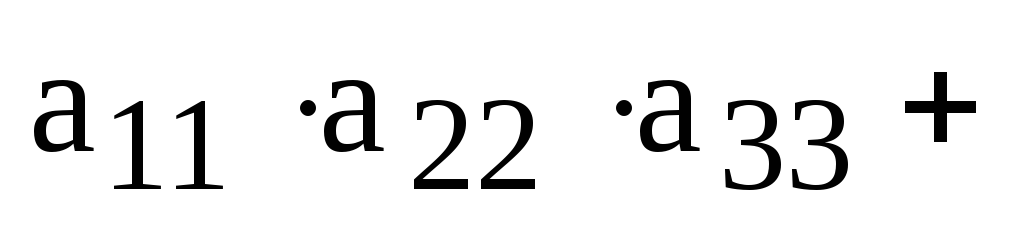
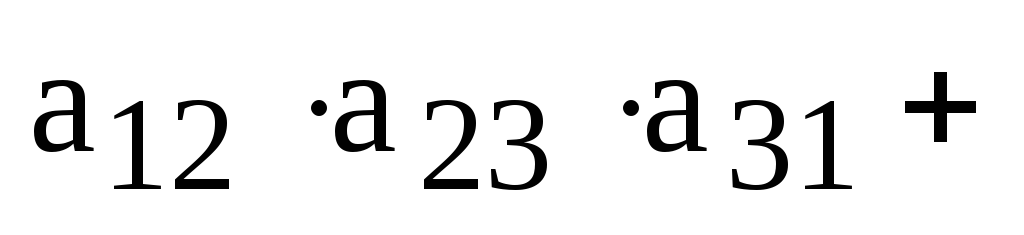
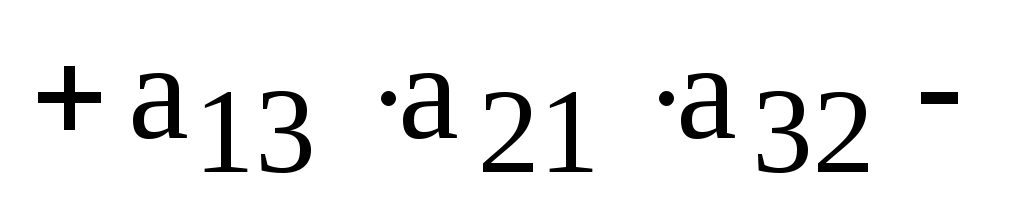
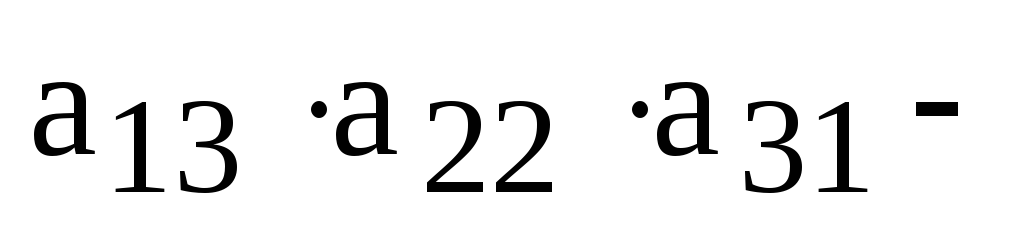
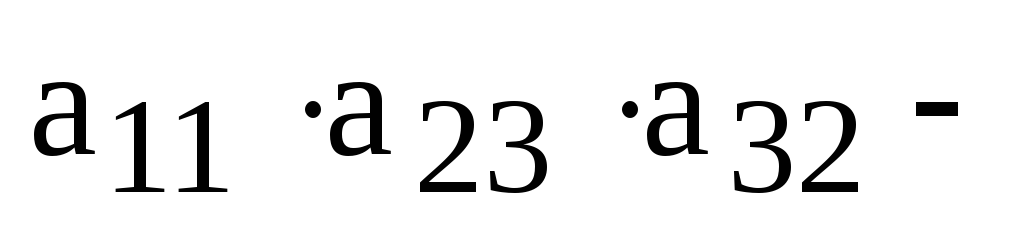
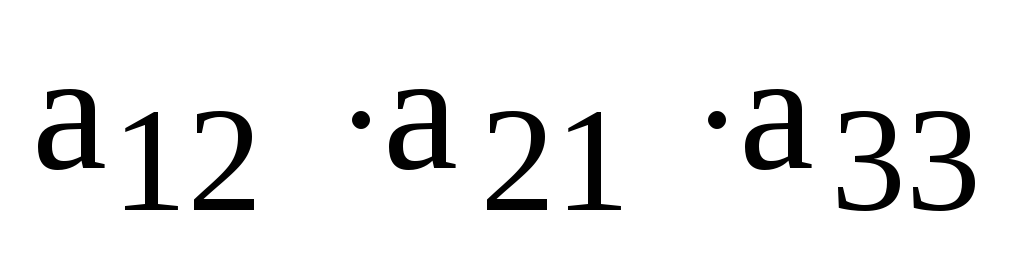 .
.
Замечание. Формула (1) определяет отображение из множества всех квадратных матриц n-го порядка над полем K в полеK. Это отображение называется определителем или детерминантом и обозначается
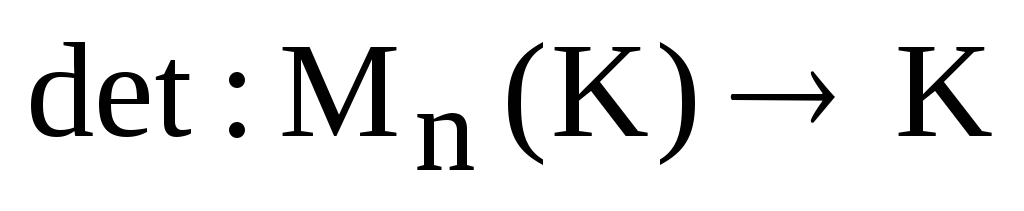 .
.
п.3. Свойства определителей.
Теорема. (Правило знаков.)
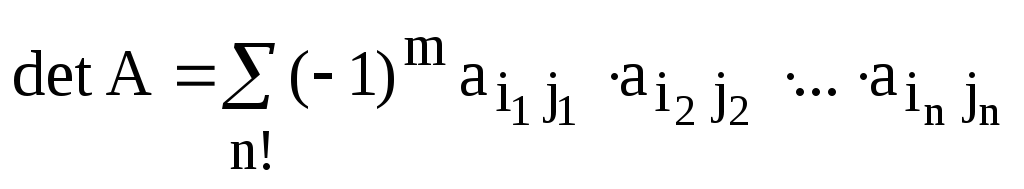 ,
(2)
,
(2)
где 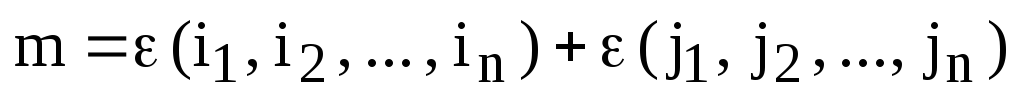 и суммирование происходит по всем членам
определителя.
и суммирование происходит по всем членам
определителя.
Доказательство.
Для того, чтобы вычислить знак члена
определителя 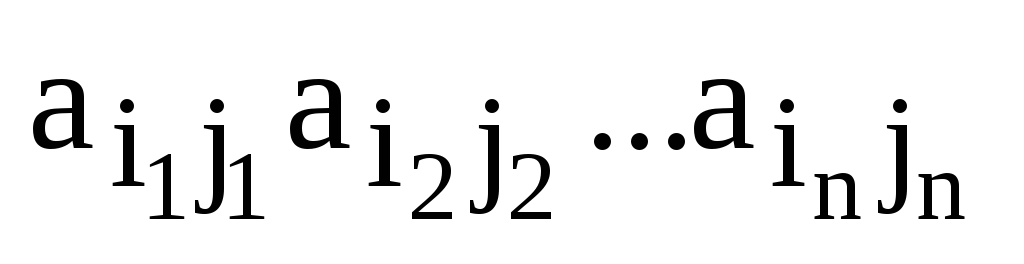 нужно упорядочить сомножители так,
чтобы индексы строк образовали начальную
перестановку
нужно упорядочить сомножители так,
чтобы индексы строк образовали начальную
перестановку 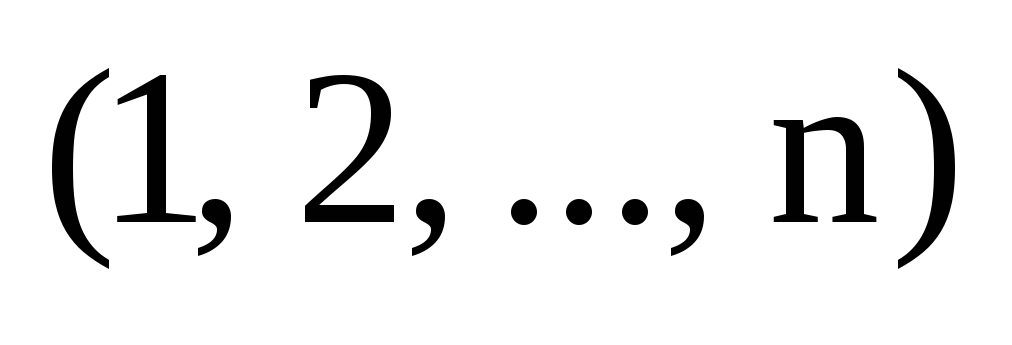 .
Этого можно добиться транспозицией
сомножителей. Допустим, что нам
потребовалось для этого t
транспозиций и мы получили член
определителя в виде
.
Этого можно добиться транспозицией
сомножителей. Допустим, что нам
потребовалось для этого t
транспозиций и мы получили член
определителя в виде 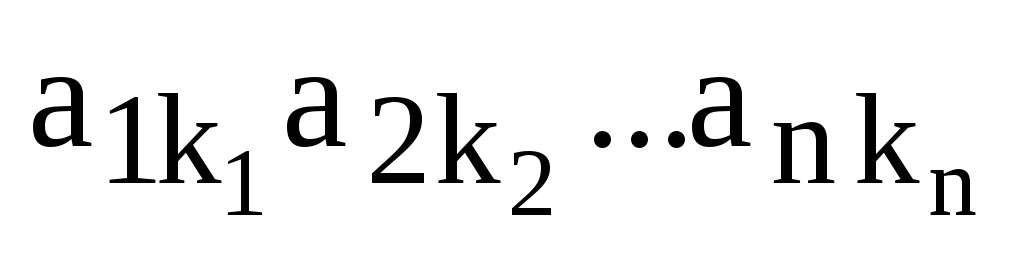 и, по определению, его знак равен
и, по определению, его знак равен 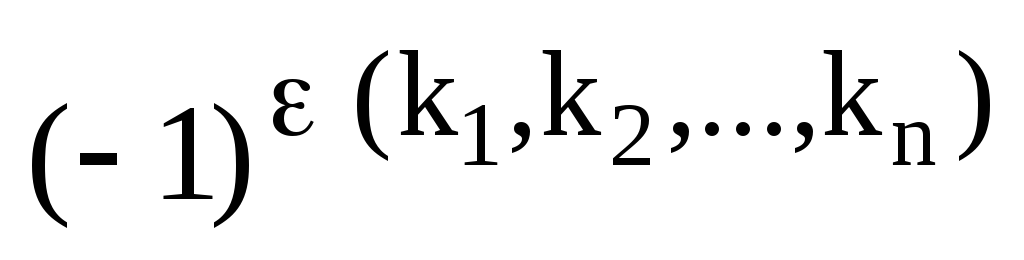 .
.
С другой стороны, первоначальные перестановки строк и столбцов претерпели изменения:
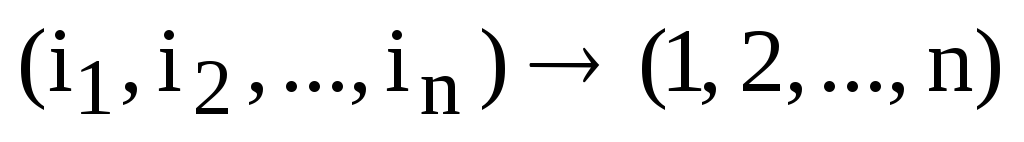 ,
, 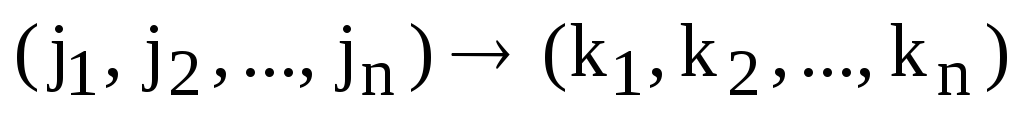 .
.
Так как этот переход произошел за t транспозиций, то четность перестановки строк не изменится, если t четное число и изменится на противоположное, если t нечетное число. Это можно отобразить формулой:
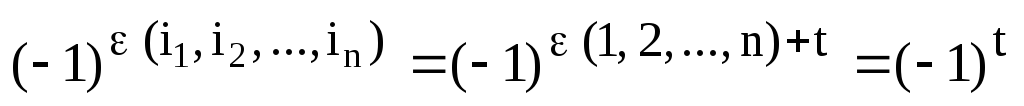 .
.
Аналогично и для перестановки столбцов
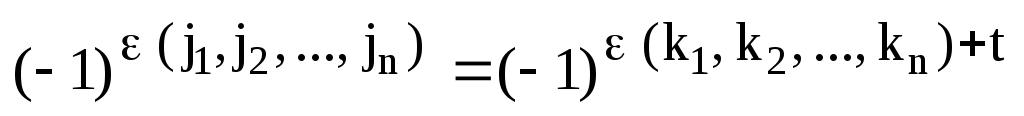 .
.
Отсюда следует, что
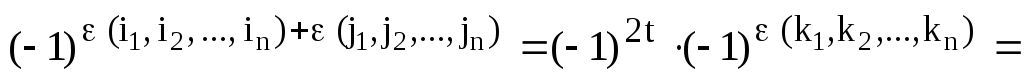
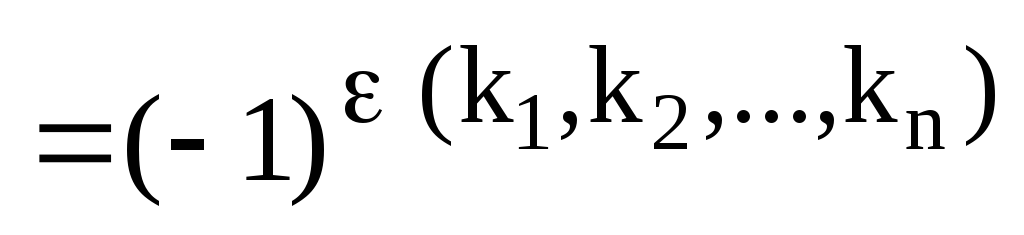 ,
ч.т.д.
,
ч.т.д.
Теорема доказана.
Теорема. (Определитель транспонированной матрицы.)
Определитель квадратной матрицы не меняется при транспонировании, т.е.
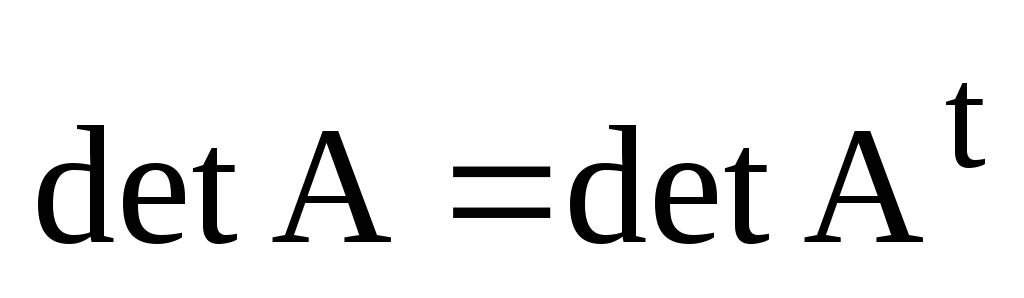 .
(3)
.
(3)
Доказательство. Пусть
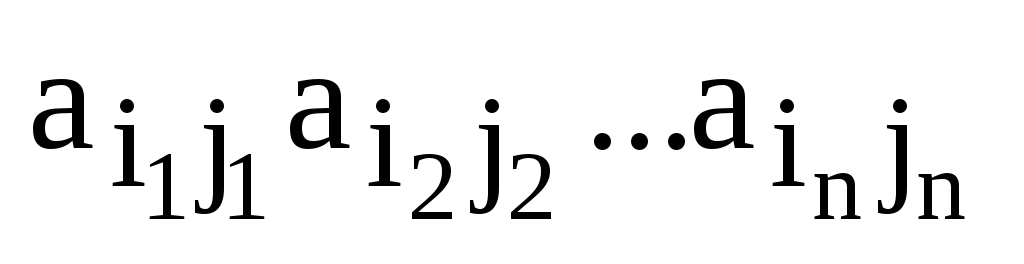 (4)
(4)
– произвольный член определителя матрицы А и
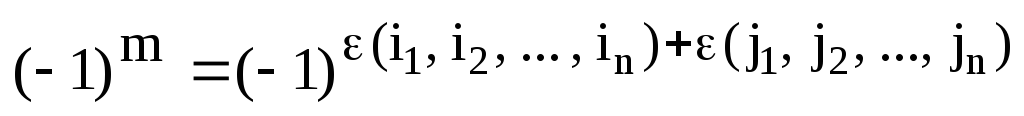 (5)
(5)
– его знак.
При транспонировании
матрицы элемент  переходит на место элемента
переходит на место элемента  ,
т.е. номер строки меняется местом с
номером столбца, поэтому произведение
(4) после транспонирования остается
членом определителя транспонированной
матрицы
,
т.е. номер строки меняется местом с
номером столбца, поэтому произведение
(4) после транспонирования остается
членом определителя транспонированной
матрицы  и он в алгебраической сумме для
определителя матрицы
и он в алгебраической сумме для
определителя матрицы  принимает вид
принимает вид
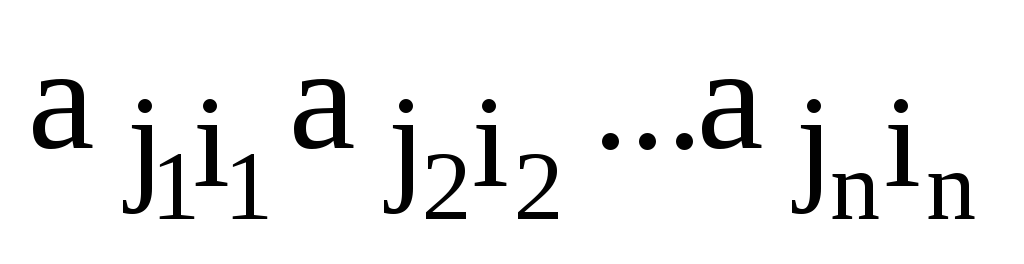 и его знак, как это
следует из формулы (5) остается прежним.
Таким образом, при транспонировании
матрицы А, каждый член определителя
матрицы А переходит в член определителя
матрицы
и его знак, как это
следует из формулы (5) остается прежним.
Таким образом, при транспонировании
матрицы А, каждый член определителя
матрицы А переходит в член определителя
матрицы  ,
причем с тем же самым знаком, откуда и
следует равенство (3).
,
причем с тем же самым знаком, откуда и
следует равенство (3).
Теорема доказана.
Замечание. Последняя теорема устанавливает равноправие строк и столбцов определителя, т.е. любое свойство определителя, которое верно для его строк остается верным и для его столбцов и наоборот.
Действительно, если какое-то свойство верно для строк любого определителя, то оно верно и для строк матрицы А и для строк матрицы , которые являются столбцами матрицы А, т.е это свойство верно и для столбцов любого определителя.
Введем обозначения.
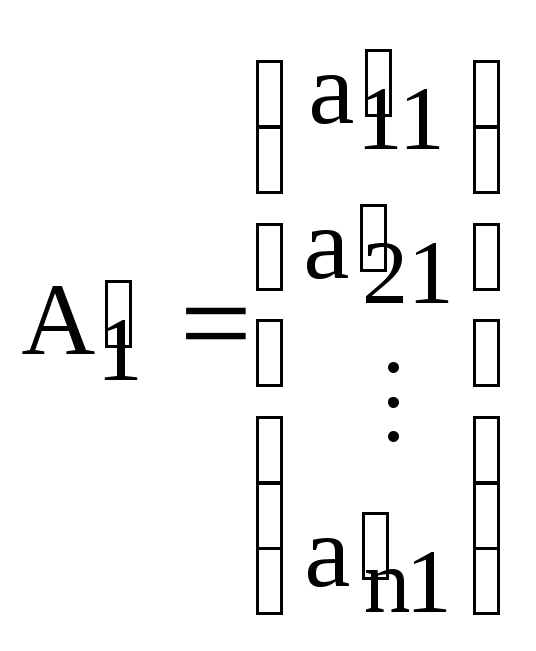
Пусть

– квадратная матрица n-го порядка.
Обозначим через 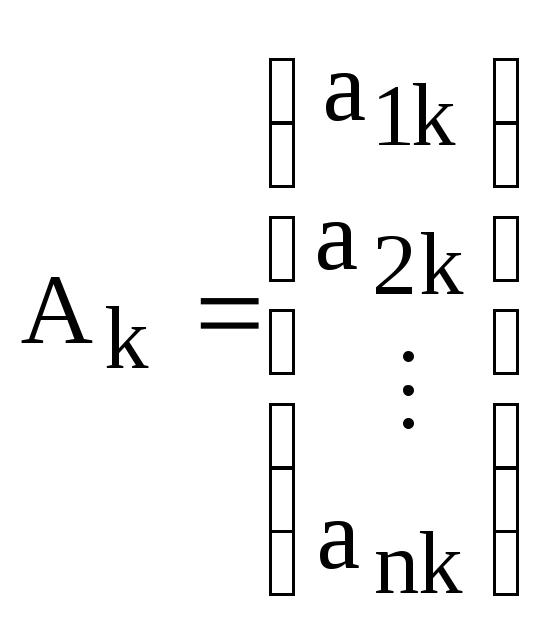 – k-й столбец матрицы А,
– k-й столбец матрицы А,
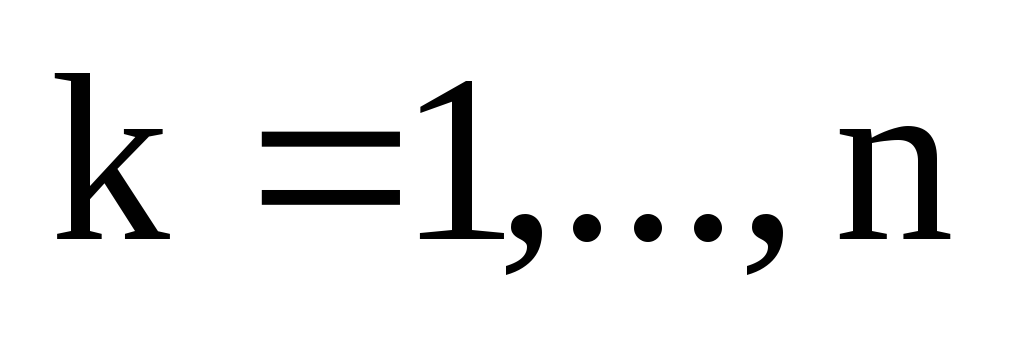 .
.
Определитель матрицы А будем также обозначать через
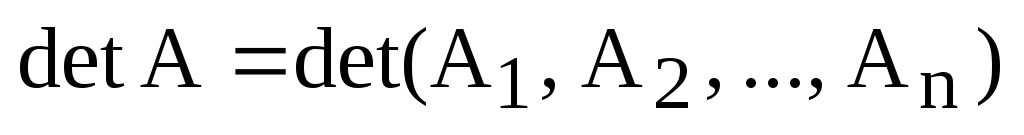 .
.
В такой форме записи определитель можно рассматривать как функцию от n переменных
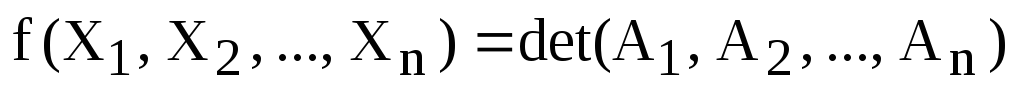 ,
,
где переменные
определены на множестве 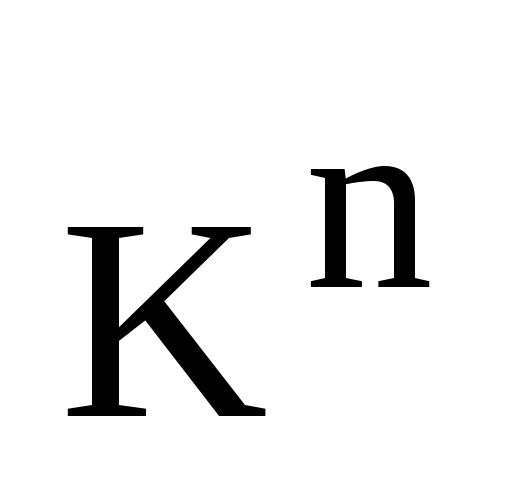 – множестве столбцов высоты n.
– множестве столбцов высоты n.
Определение.
Функция от n переменных 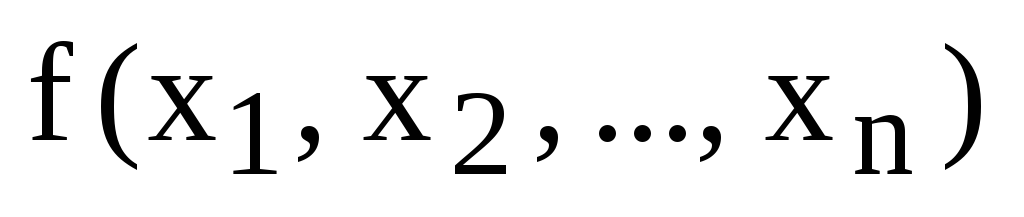 называется линейная по k-му
аргументу, если выполняются следующие
два свойства:
называется линейная по k-му
аргументу, если выполняются следующие
два свойства:
1) для любых значений
k-й переменной 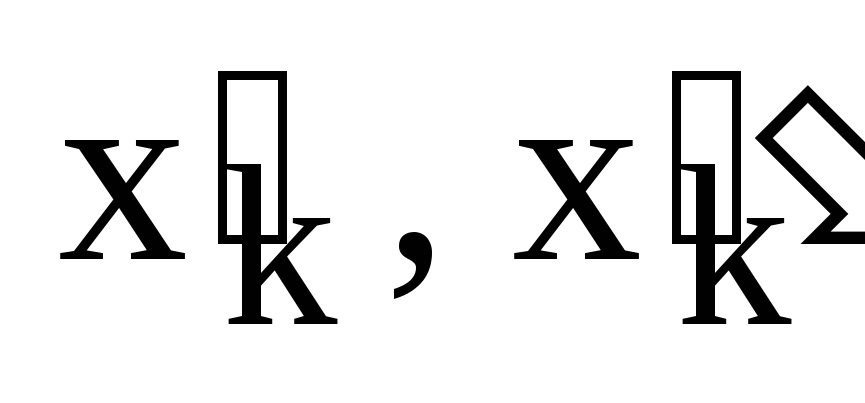 ,
взятых из области определения k-й
переменной верно равенство
,
взятых из области определения k-й
переменной верно равенство
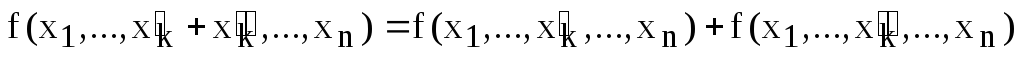 ;
;
2) для любого скаляра  и для любого значения k-й
переменной
и для любого значения k-й
переменной 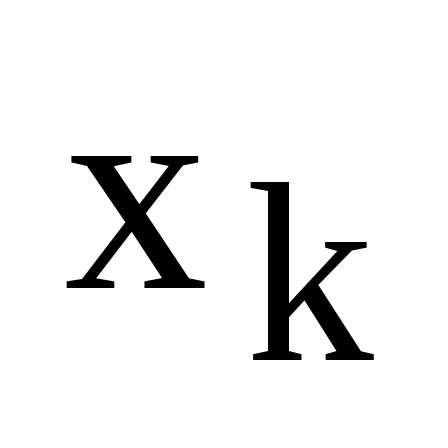 ,
взятого из области определения k-й
переменной верно равенство
,
взятого из области определения k-й
переменной верно равенство
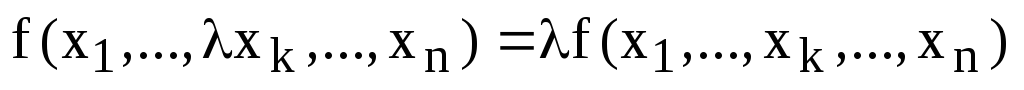 .
.
Определение. Функция от нескольких переменных, которая линейна по каждому своему переменному, называется полилинейной.
Теорема. (Свойство линейности определителя.)
Определитель
квадратной матрицы над полем K
является полилинейной функцией своих
столбцов, т.е. 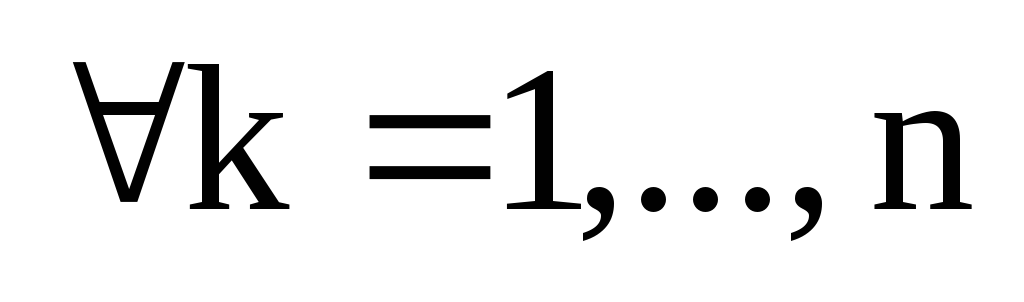 :
:
1) 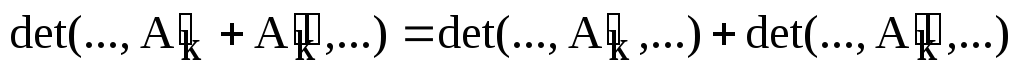 ;
;
2)  ,
, 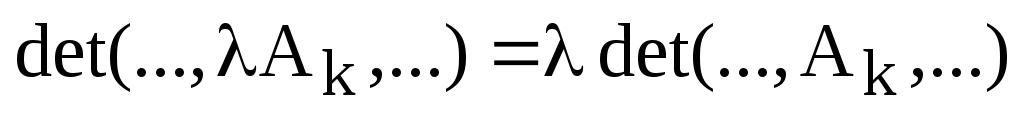 .
.
Доказательство.
Пусть, для удобства записи, 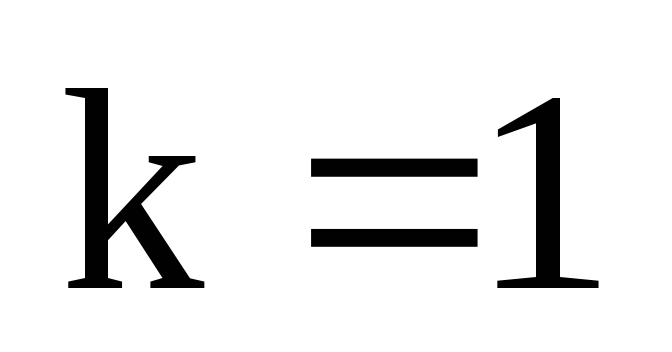 и
и
 .
.
Обозначим
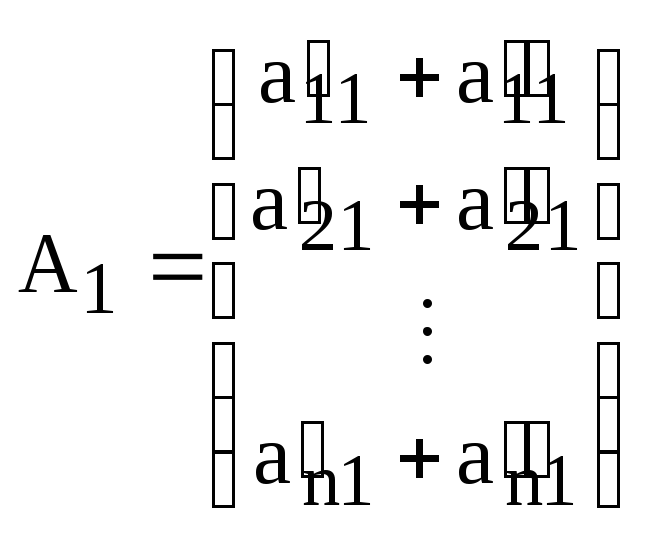 ,
,  ,
, 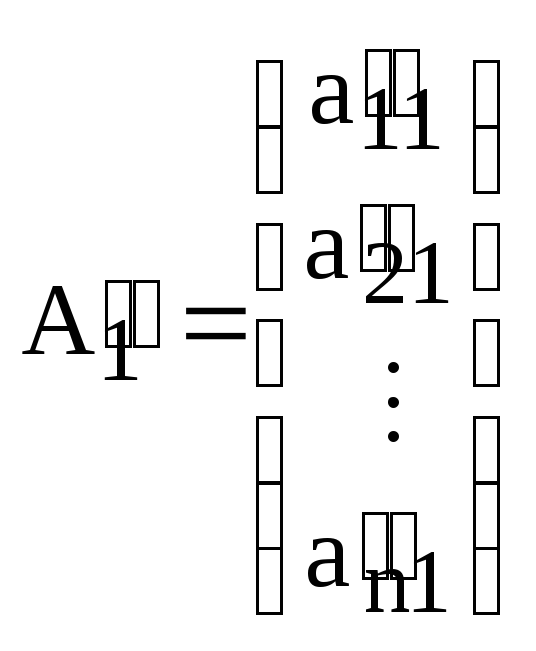 .
.
Тогда 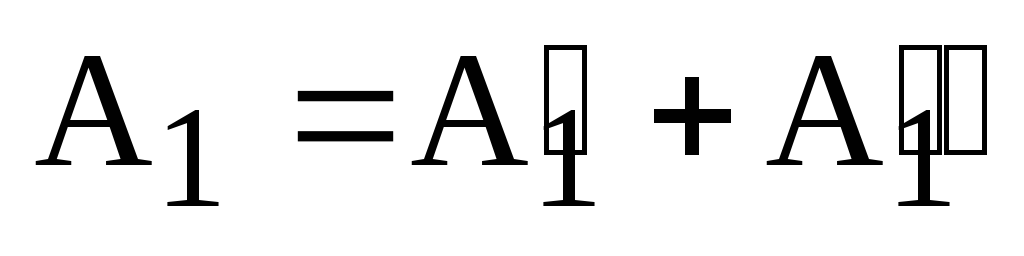 и
и
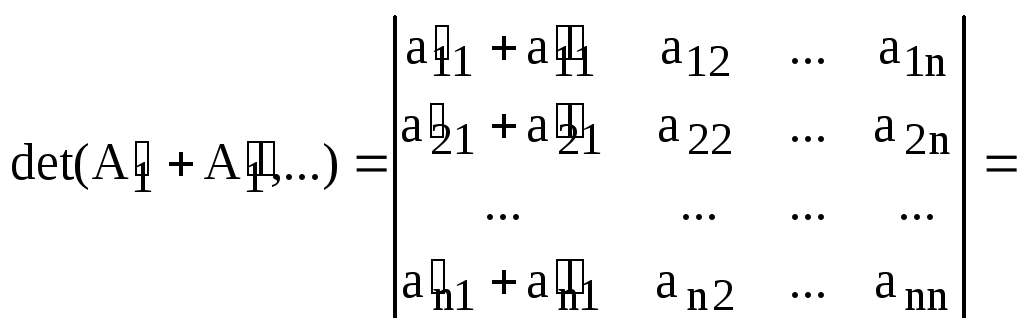 .
.
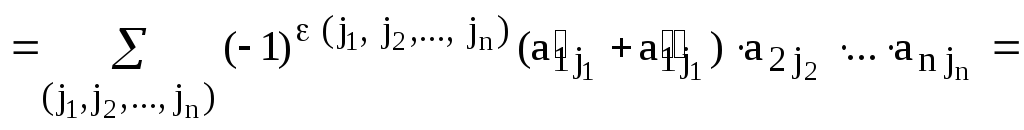
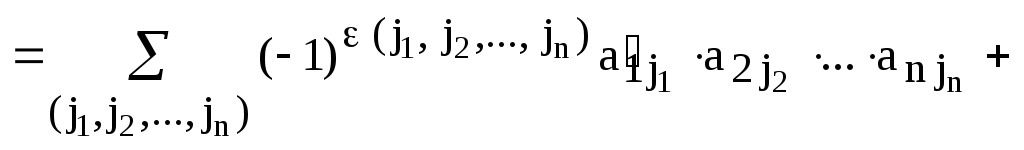
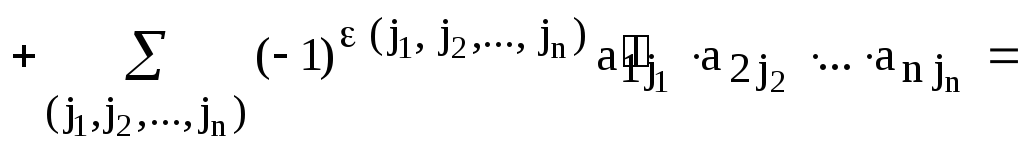


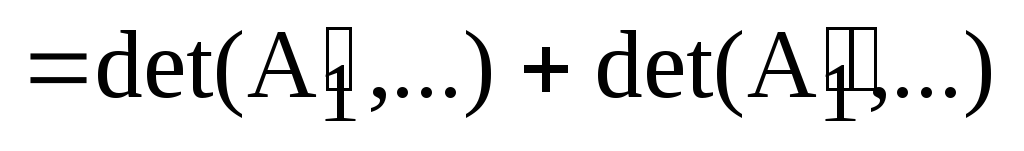 .
.
Аналогично доказывается второе равенство.
Теорема доказана.
Определение. Два столбца определителя называются пропорциональными, если один из них можно получить из другого умножением на ненулевой скаляр:
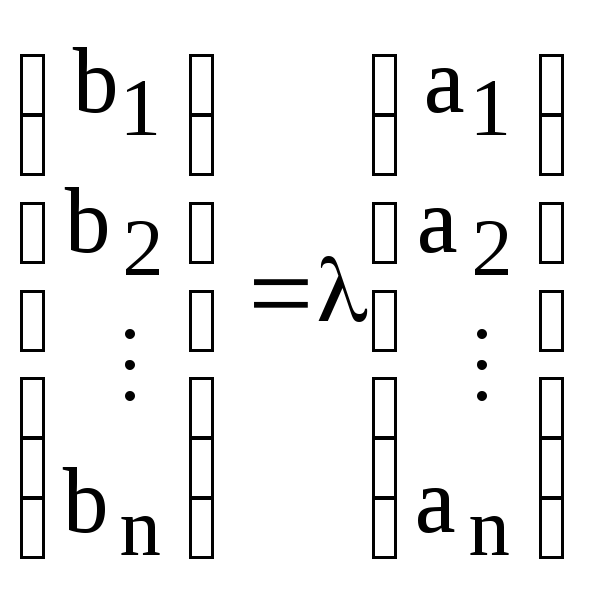 ,
,
где 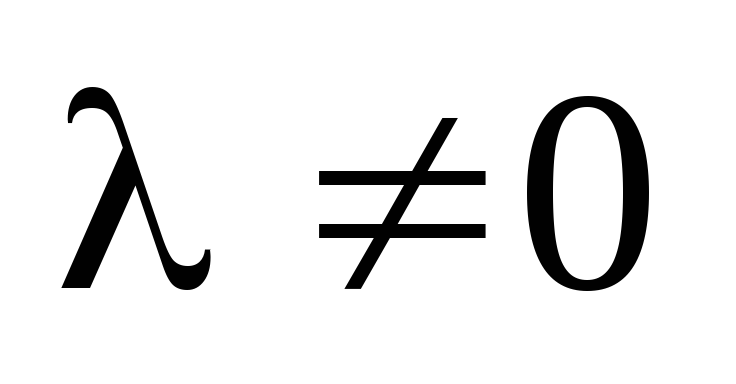 .
.
Аналогично определяется понятие пропорциональных строк.
Определение. Пусть 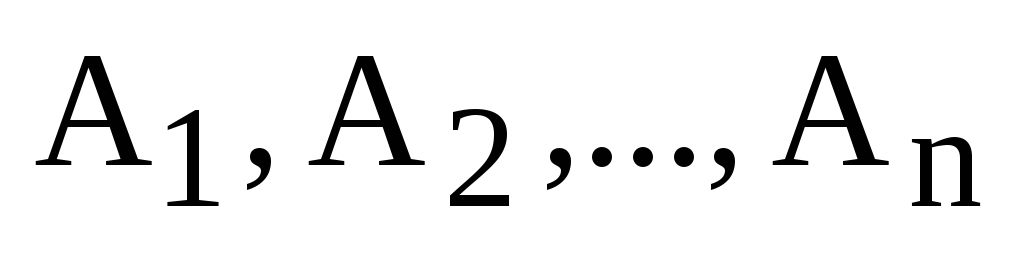 – столбцы определителя (матрицы).
Линейной комбинацией столбцов называется
столбец равный
– столбцы определителя (матрицы).
Линейной комбинацией столбцов называется
столбец равный
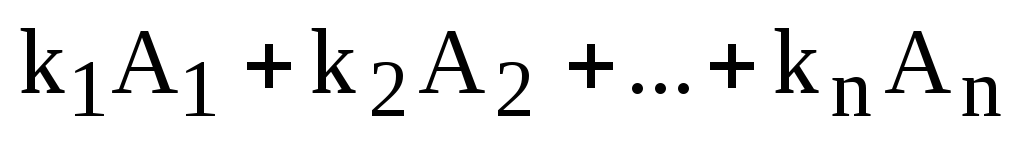 ,
,
где 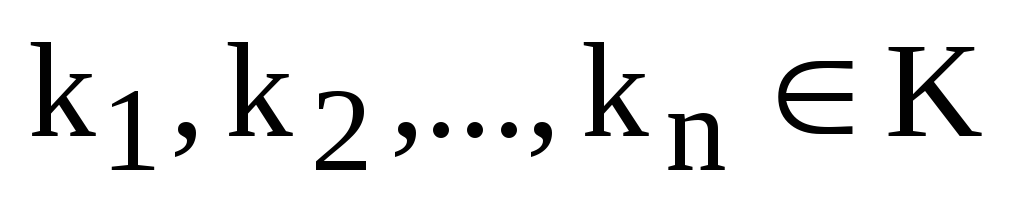 –
произвольные скаляры.
–
произвольные скаляры.
Аналогично определяется понятие пропорциональных строк и понятие линейной комбинации строк.
Теорема. (Свойства определителя.)
1. Определитель, имеющий нулевой столбец (нулевую строку) равен нулю.
2. Определитель меняет знак при любой транспозиции его столбцов (строк).
3. Определитель, имеющий два равных столбца (две равные строки), равен нулю.
4. Определитель, имеющий два пропорциональных столбца (строки), равен нулю.
5. Определитель не меняет своего значения, если к какому-либо его столбцу (строке) прибавить любую линейную комбинацию других его столбцов (строк).
Доказательство. В силу равноправности строк и столбцов любое свойство достаточно доказать или для строк или для столбцов.
1) Пусть определитель имеет нулевой столбец. Каждый член определителя имеет точно один множитель из нулевого столбца и поэтому равен нулю. Следовательно, и определитель равен нулю.
2) Докажем это свойство для строк.
Пусть в определителе
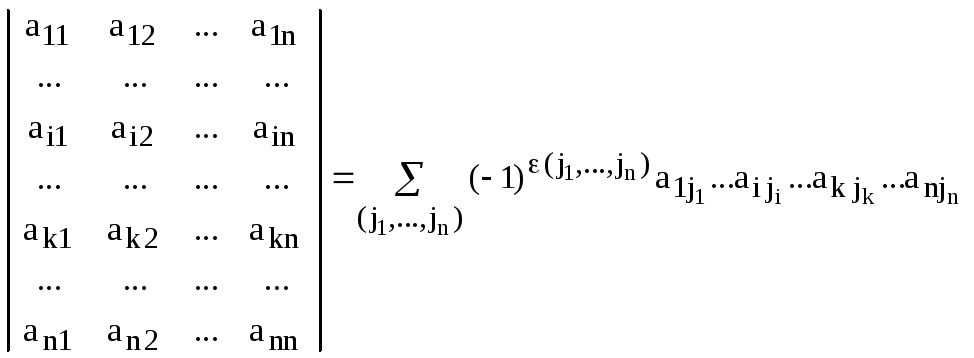
переставили местами i-ю и k-ю строки:
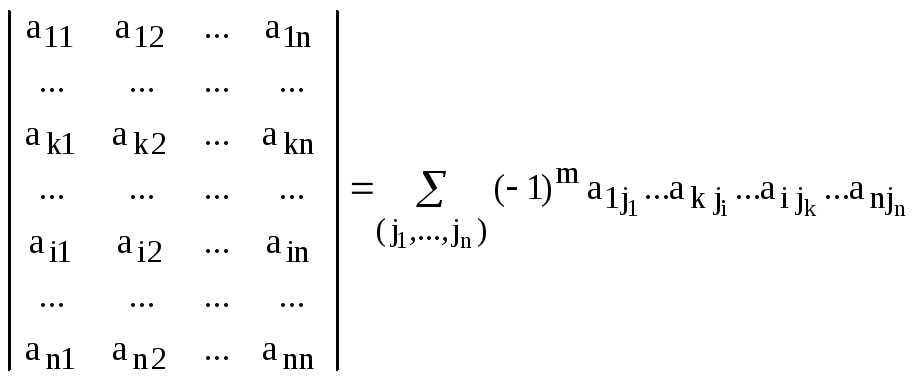 ,
,
где
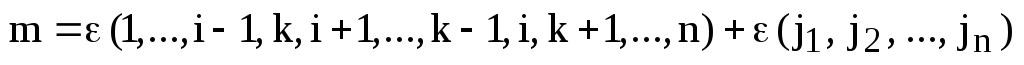 .
.
Мы видим, что в начальной перестановке строк
(1, …, i-1, i, i+1, …, k-1, k, k+1, …, n)
произошла транспозиция (i k):
(1, …, i-1, k, i+1, …, k-1, i, k+1, …, n).
Первоначальная перестановка является четной, а после транспозиции (i k) перестановка получается нечетной.
Следовательно,
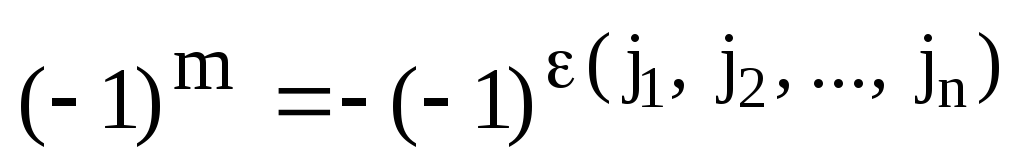 .
.
Таким образом, при такой перестановке строк каждый член определителя меняет свой знак на противоположный, откуда и следует первое утверждение теоремы.
3) Пусть определитель имеет два равных строки.
Переставим их друг с другом. С одной стороны, определитель изменил свой знак на противоположный, а с другой стороны матрица осталась прежней, в силу равенства переставляемых строк, откуда следует, что
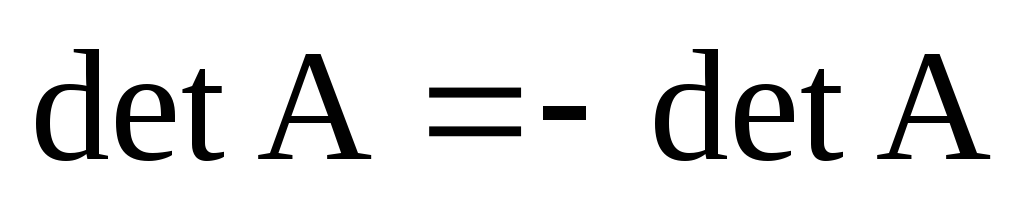 .
.
Если в поле K
верно неравенство 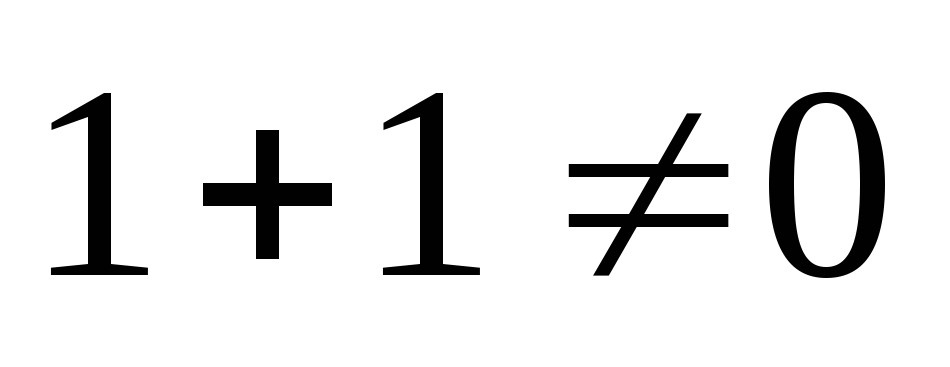 ,
т.е. характеристика поля не равна 2, тогда
получаем:
,
т.е. характеристика поля не равна 2, тогда
получаем:
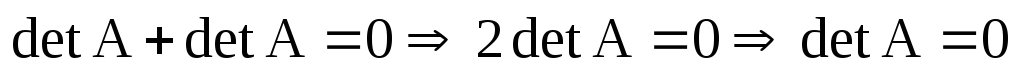
и утверждение доказано.
Пусть в определителе
равны строки с номерами i
и k, 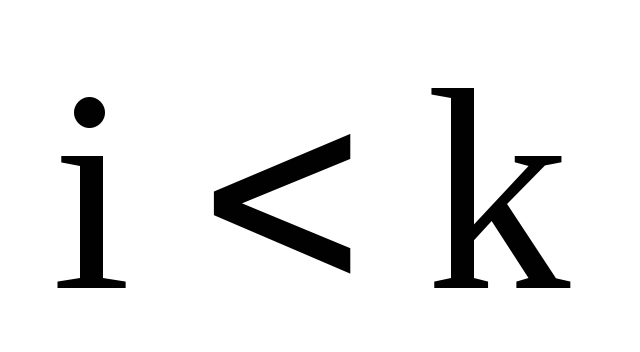 ,
и пусть характеристика поля равна 2,
т.е.
,
и пусть характеристика поля равна 2,
т.е. 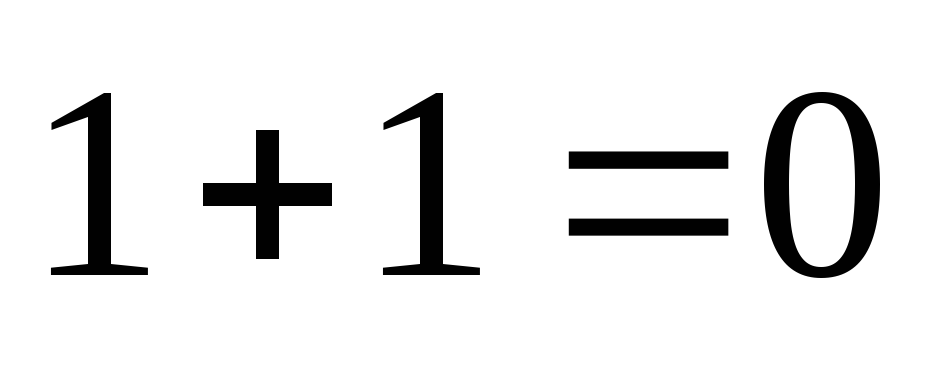 ,
тогда
,
тогда 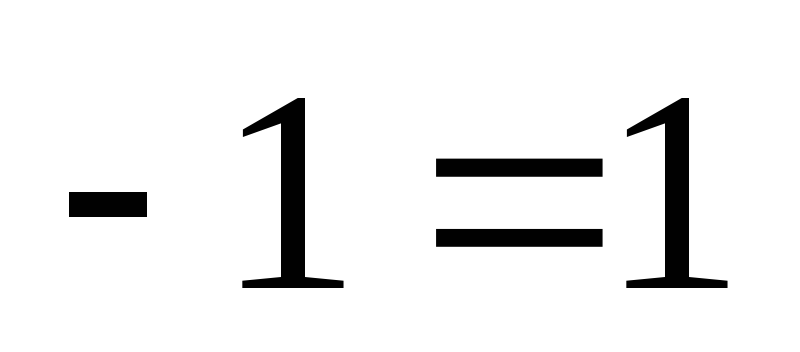 и все члены определителя имеют одинаковый
знак.
и все члены определителя имеют одинаковый
знак.
Каждый член
определителя содержит ровно один элемент
из i-й строки, например, 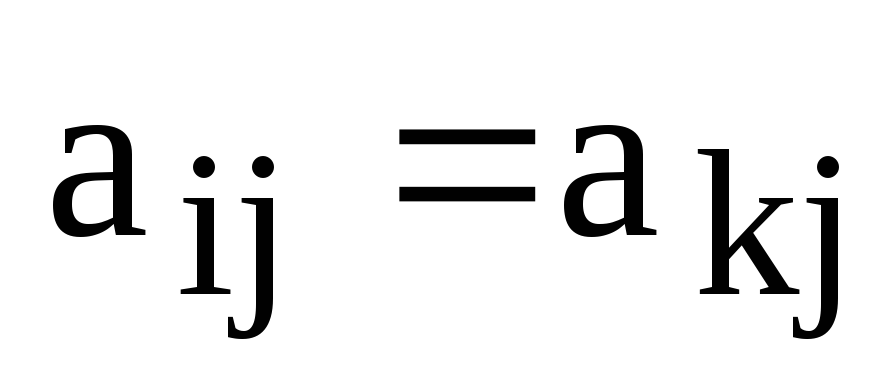 и ровно один элемент из k-й
строки, например,
и ровно один элемент из k-й
строки, например, 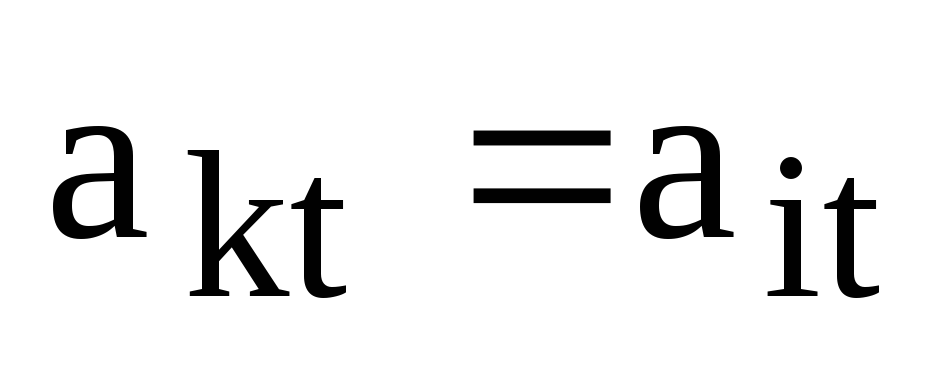 ,
причем,
,
причем, 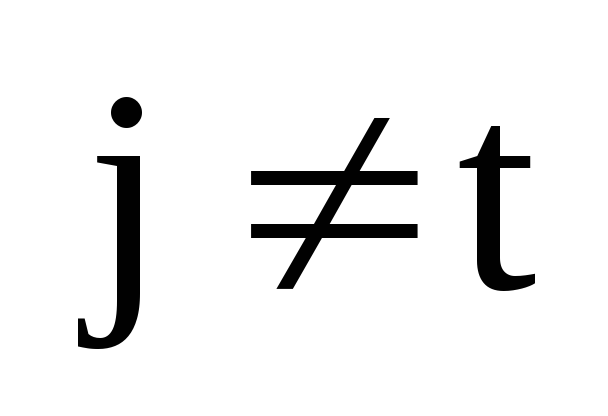 .
Переставим в члене определителя
.
Переставим в члене определителя
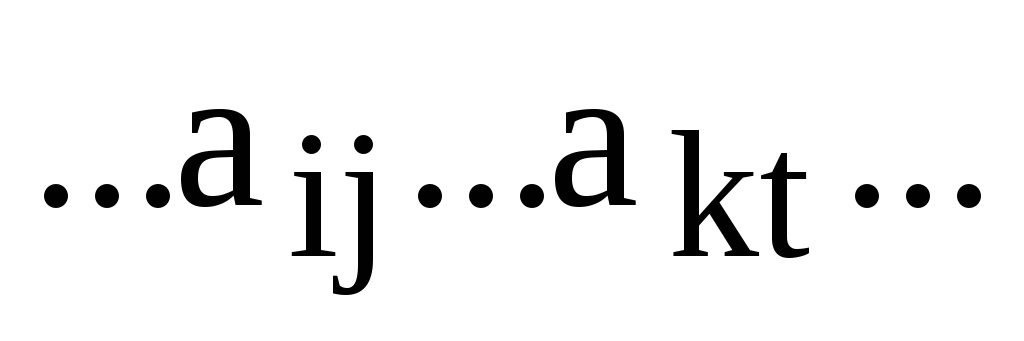
эти сомножители друг с другом:
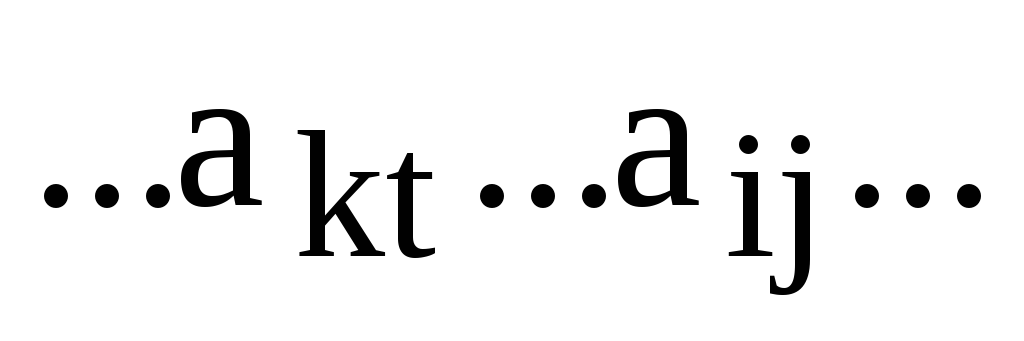
Так как 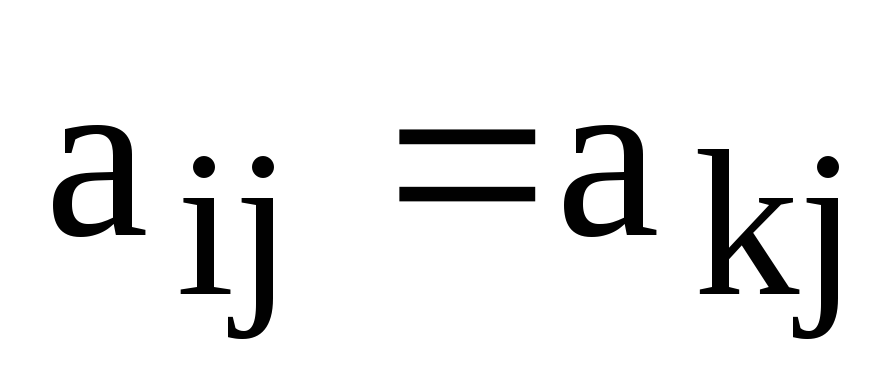 и
и 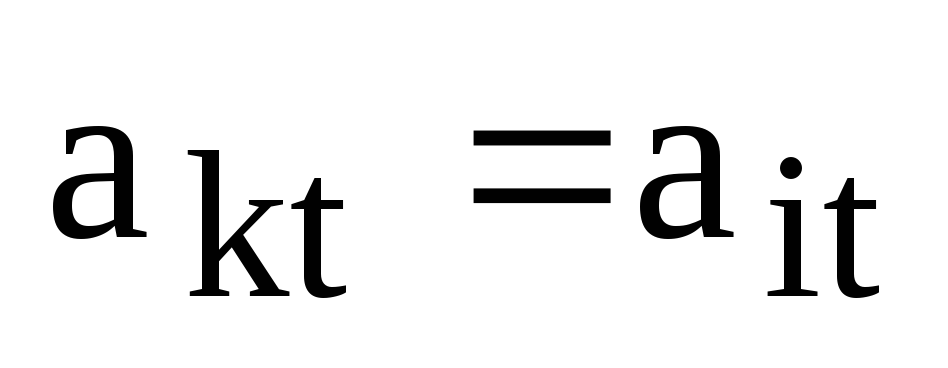 ,
то последний член определителя равен
,
то последний член определителя равен
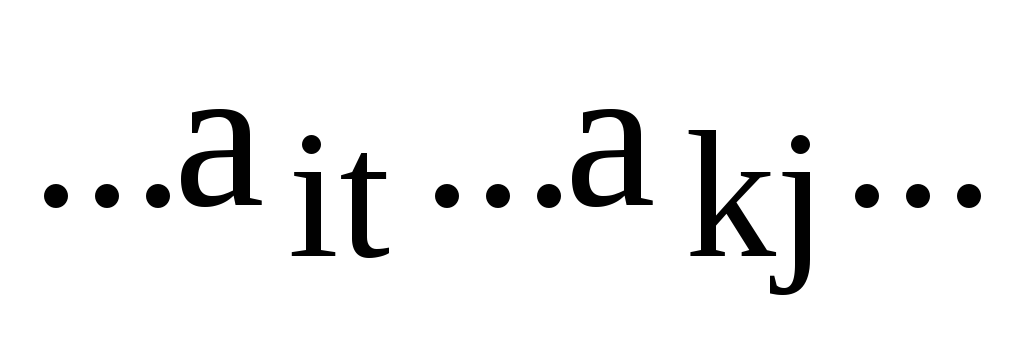
Таким образом, получаем, что, с одной стороны, член определителя не изменится (от перестановки множителей произведение не меняется), а с другой стороны это другой член определителя, т.к. элементы из i-й и k-й строк взяты из других столбцов.
Получается, что каждый член определителя встречается в алгебраической сумме дважды. Но в поле характеристики 2 сумма двух одинаковых слагаемых равна нулю:
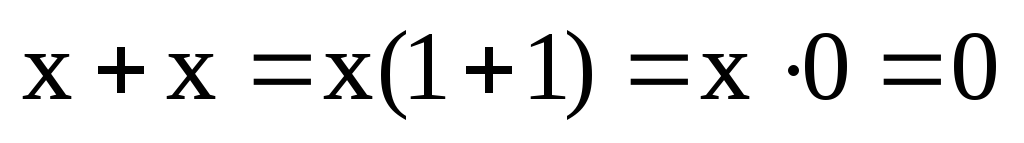 .
.
Тем самым и определитель равен нулю, ч.т.д.
4) Пусть в определителе
пропорциональны столбцы с номерами j
и k. Это означает, что 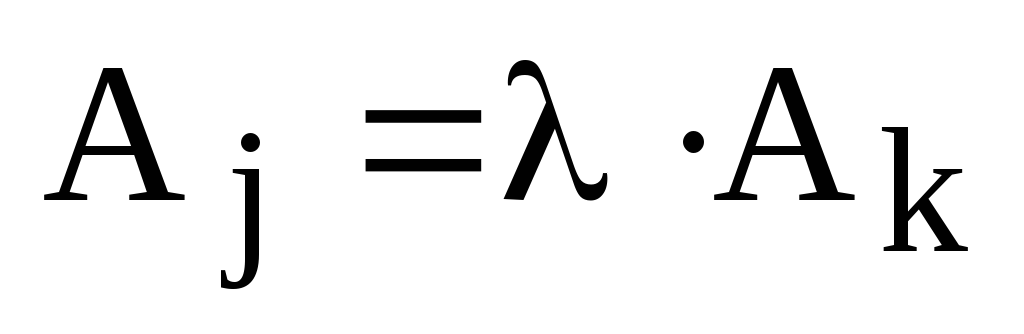 для некоторого скаляра
для некоторого скаляра 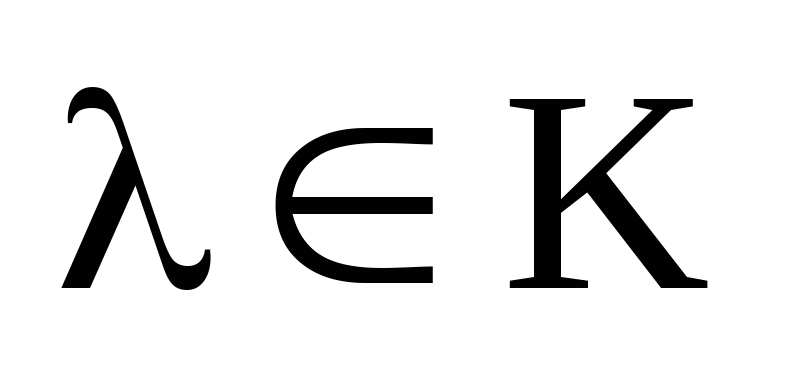 .
Тогда по уже доказанным свойствам
.
Тогда по уже доказанным свойствам
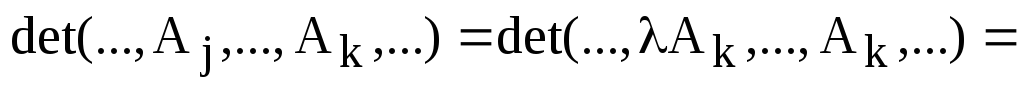
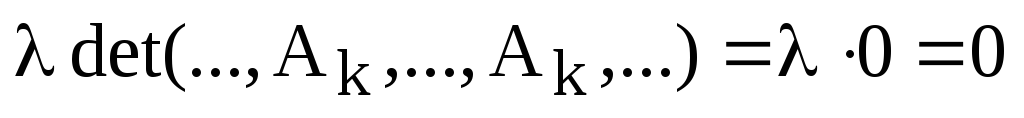 ,
ч.т.д.
,
ч.т.д.
5) Для простоты записи, допустим, что к первому столбцу определителя мы прибавили линейную комбинацию других столбцов этого же определителя. Используя доказанные свойства, получаем:
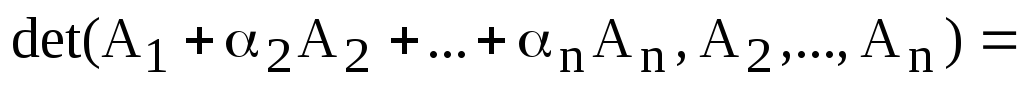
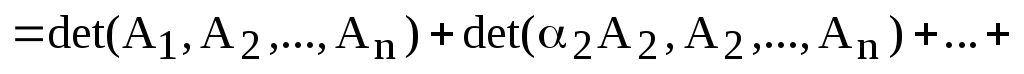
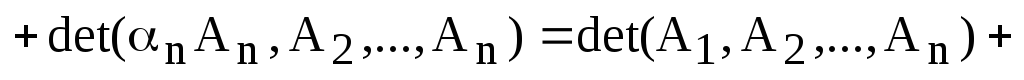
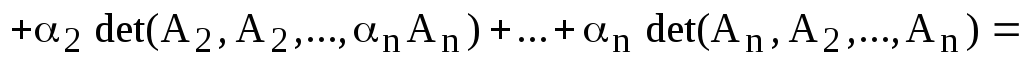
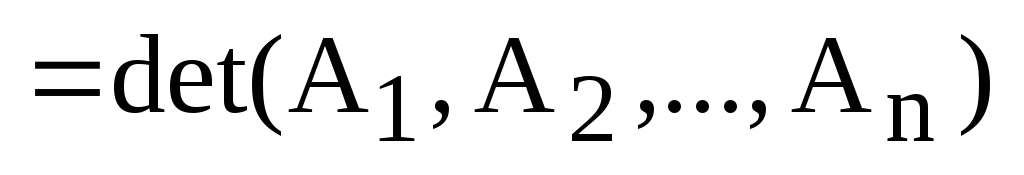 .
.
Теорема доказана.
Определение. Пусть
дана система столбцов (строк) 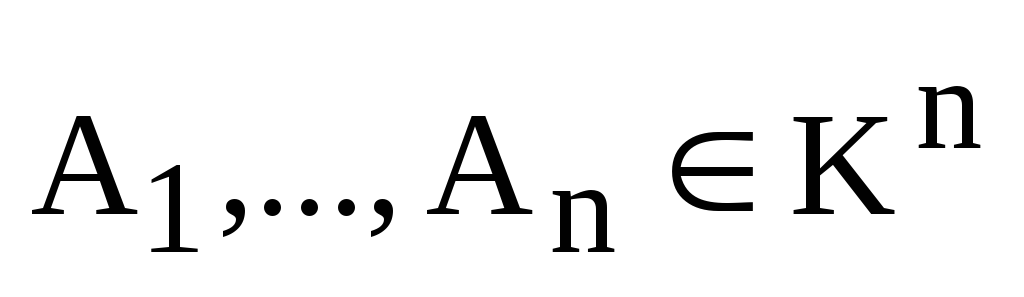 .
Линейной комбинацией данной системы
называется выражение
.
Линейной комбинацией данной системы
называется выражение
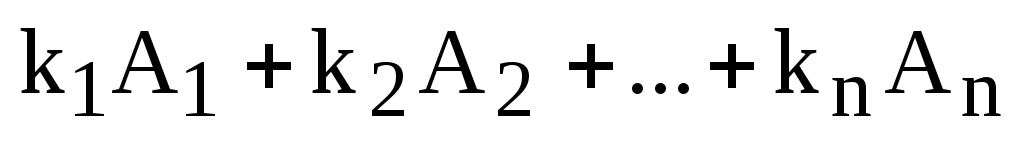 ,
,
где 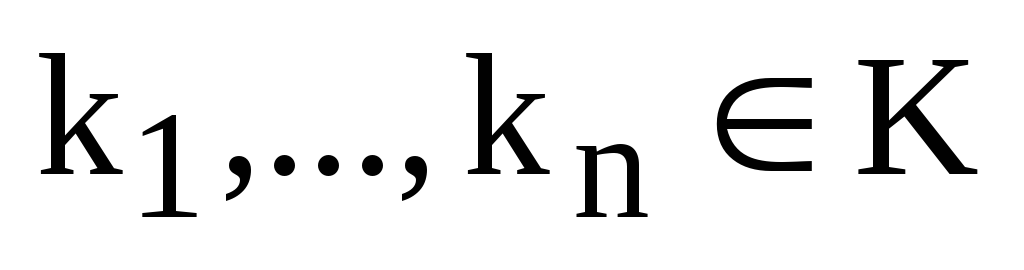 скаляры из поля K, которые
называются коэффициентами этой линейной
комбинации.
скаляры из поля K, которые
называются коэффициентами этой линейной
комбинации.
Определение. Система столбцов (строк) называется линейно зависимой, если существует их линейная комбинация равная нулевому столбцу (нулевой строке), причем хотя бы один из коэффициентов этой линейной комбинации не равен 0:
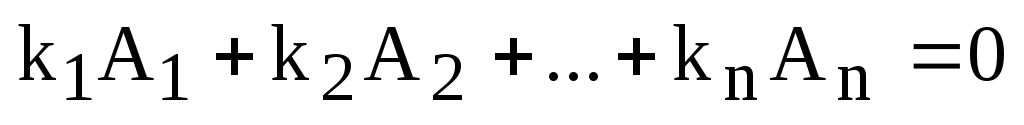 .
.
В противном случае данная система столбцов (строк) называется линейно независимой.
Теорема. Если система столбцов (строк) определителя линейно зависимая, тогда определитель равен нулю.
Доказательство. Пусть система линейно зависимая и
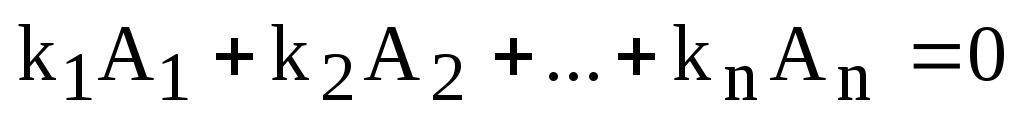 ,
,
где 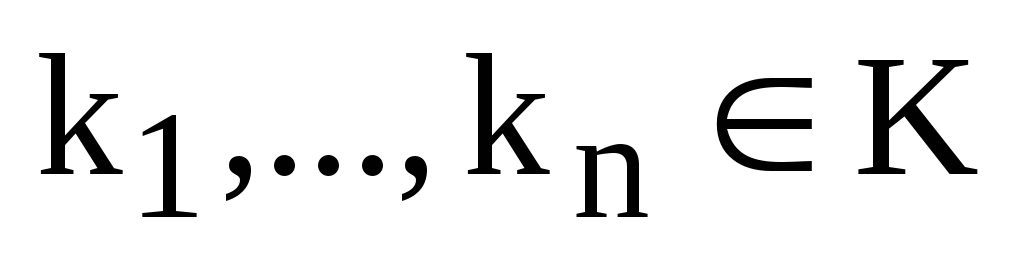 .
Пусть, для определенности,
.
Пусть, для определенности, 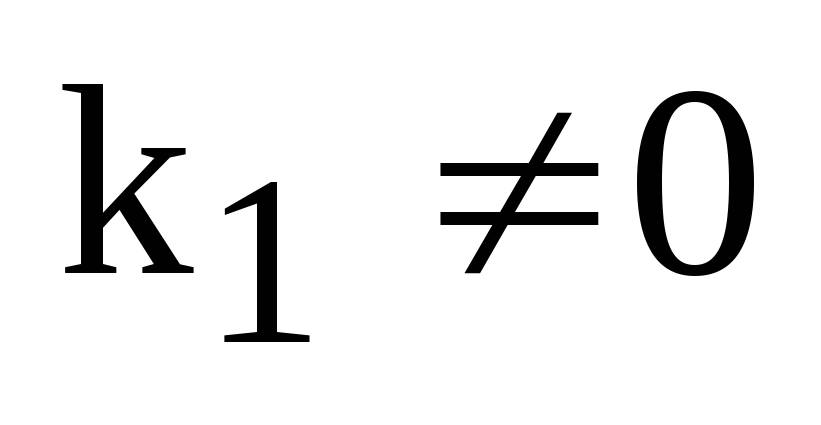 .
Тогда
.
Тогда
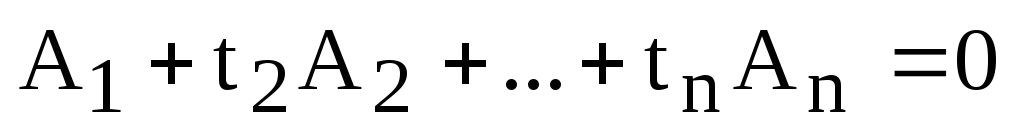 ,
,
Чередующаяся перестановка — Википедия
Эта статья о перестановках, элементы которых по очереди возрастают и убывают; о перестановках, в которых элементы по очереди чётны и нечётны см. Меандровая перестановка.| n{\displaystyle n} | Чередующиеся перестановки | Обратно чередующиеся перестановки | Количество An{\displaystyle A_{n}} |
|---|---|---|---|
| 2 | (2,1) | (1,2) | 2 |
| 3 | (2,1,3), (3,1,2) | (1,3,2), (2,3,1) | 4 |
| 4 | (2,1,4,3), (3,1,4,2), (3,2,4,1), (4,1,3,2), (4,2,3,1) | (1,3,2,4), (1,4,2,3), (2,3,1,4), (2,4,1,3), (3,4,1,2) | 10 |
 Геометрическое изображение всех чередующихся перестановок пяти элементов. Перестановки лексикографически упорядочены — от (1,3,2,5,4) (сверху слева) до (4,5,2,3,1) (снизу справа).
Геометрическое изображение всех чередующихся перестановок пяти элементов. Перестановки лексикографически упорядочены — от (1,3,2,5,4) (сверху слева) до (4,5,2,3,1) (снизу справа).Чередующаяся перестановка[1] (перестановка down-up; иногда альтернирующая перестановка от англ. alternating permutation или пилообразная перестановка) — перестановка a{\displaystyle a}, такая что её члены по очереди возрастают и убывают, начиная с убывания:
- a1>a2<a3>a4<…{\displaystyle a_{1}>a_{2}<a_{3}>a_{4}<\ldots }.
Обратно чередующаяся перестановка (перестановка up-down) a{\displaystyle a} — такая, что её члены по очереди возрастают и убывают, начиная с возрастания:
- a1<a2>a3<a4>…{\displaystyle a_{1}<a_{2}>a_{3}<a_{4}>\ldots }.
Иногда условие того, начинается ли чередование с возрастания или убывания, опускают, и оба варианта называют чередующимися перестановками без уточнения.
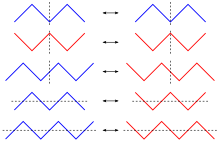 Горизонтальное и вертикально отражений чередующихся (красных) и обратно чередующихся (синих) перестановок.
Горизонтальное и вертикально отражений чередующихся (красных) и обратно чередующихся (синих) перестановок.Чередующиеся перестановки могут быть изображены геометрически как пилообразная кривая (см. рисунок справа). На них существует два биективных отображения — отражение относительно горизонтали или вертикали. При этом горизонтальное отражение переводит чередующиеся в чередующиеся для нечётной длины и в обратно чередующиеся для чётной, а вертикальное — всегда в обратно чередующиеся. В частности, число чередующихся и число обратно чередующихся перестановок на одном количестве элементов одинаково[2].
Числа An{\displaystyle A_{n}} чередующихся перестановок на n{\displaystyle n} элементах образуют последовательность, начинающуюся c 1, 1, 1, 2, 5, 16, 61, 272, 1385, 7936, 50521, …, см. последовательность A000111 в OEIS.
Разбивая чередующиеся или обратно чередующиеся перестановки по положению элемента 1{\displaystyle 1}, можно показать, что эта последовательность удовлетворяет рекуррентному соотношению[1]
- 2An+1=∑i=0n(ni)AiAn−i{\displaystyle 2A_{n+1}=\sum _{i=0}^{n}{\binom {n}{i}}A_{i}A_{n-i}}.
Таким образом, экспоненциальная производящая функция A(x)=∑n≥0Anxn/n!{\displaystyle A(x)=\sum _{n\geq 0}A_{n}x^{n}/n!} этой последовательности удовлетворяет дифференциальному уравнению
- 2A′(x)=1+(A(x))2{\displaystyle 2A'(x)=1+(A(x))^{2}}
с начальным условием A(0)=1{\displaystyle A(0)=1}[3]. Из этого можно вывести, что она равна A(x)=tgx+secx{\displaystyle A(x)=\mathrm {tg} x+\sec x}[1].
Секанс чётен, а тангенс — нечётен, поэтому чётные члены последовательности совпадают с коэффициентами в ряде Тейлора секанса, а нечётные — тангенса, а потому выражаются через числа Бернулли и числа Эйлера соответственно, см. подробности в Тригонометрические функции#Определение тригонометрических функций через ряды.
Ассимптотически последовательность An{\displaystyle A_{n}} равна
- Ann!≃2(2π)n+1{\displaystyle {\frac {A_{n}}{n!}}\simeq 2\left({\frac {2}{\pi }}\right)^{n+1}}.
Число справа примерно равно вероятности того, что перестановка чередующаяся[4].
Числа Энтрингера (англ. Entringer numbers) — это числа An,k{\displaystyle A_{n,k}} чередующихся перестановок n{\displaystyle n} элементов, начинающихся с k{\displaystyle k}. Таким образом,
- An=∑k=1nAn,k{\displaystyle A_{n}=\sum _{k=1}^{n}A_{n,k}}.
Кроме того, поскольку к любой обратно чередующейся последовательности можно прибавить в начале (n+1){\displaystyle (n+1)}, и получить чередующуюся последовательность,
- An+1,n+1=An{\displaystyle A_{n+1,n+1}=A_{n}},
а потому числа чередующихся последовательностей — частный случай чисел Энтрингера.
Числа Энтрингена удовлетворяют рекуррентному соотношению
- An,k=An,k−1+An−1,n−k+1{\displaystyle A_{n,k}=A_{n,k-1}+A_{n-1,n-k+1}}
и потому образуют треугольник наподобие треугольника Паскаля (см. справа). Последовательность, получающаяся при его построчном перечислении с пропуском нулей, — это последовательность A008282 в OEIS[5].
Перестановка — это… Что такое Перестановка?
В комбинаторике перестано́вка — это упорядоченный набор чисел обычно трактуемый как биекция на множестве , которая числу i ставит соответствие i-й элемент из набора. Число n при этом называется порядком перестановки. Как синоним слову «перестановка» в этом смысле некоторые авторы используют слово расстановка.
В теории групп под перестановкой произвольного множества подразумевается биекция этого множества на себя. Как синоним слову «перестановка» в этом смысле некоторые авторы используют слово подстановка. (Другие авторы подстановкой называют наглядный способ записи перестановки.)
Свойства
Связанные определения
Специальные типы перестановок
Подстановки и произведения циклов
Перестановка множества может быть записана в виде подстановки, например:
где и
Перестановку также можно записать в виде произведения непересекающихся циклов, причём единственным образом с точностью до порядка следования циклов в произведении. Например:
Перестановки с повторением
Рассмотрим n элементов m различных типов, причем в каждом типе все элементы одинаковы. Тогда перестановки из всех этих элементов с точностью до порядка следования однотипных элементов называются перестановками с повторением. Если ki — количество элементов i-го типа, то и количество всевозможных перестановок с повторениями равно мультиномиальному коэффициенту
Случайная перестановка
Случайной перестановкой называется случайный вектор все элементы которого принимают натуральные значения от 1 до и при этом вероятность совпадения любых двух элементов равна 0.
Независимой случайной перестановкой называется такая случайная перестановка , для которой
для некоторых таких что
Если при этом не зависят от , то перестановку называют одинаково распределённой. Если же нет зависимости от , то есть то называют однородной.
См. также
Примечания
Литература
- Дональд Кнут Искусство программирования, том 3. Сортировка и поиск = The Art of Computer Programming, vol.3. Sorting and Searching. — 2-е изд. — М.: «Вильямс», 2007. — С. 824. — ISBN 0-201-89685-0
Ссылки
Инверсия (перестановка) — это… Что такое Инверсия (перестановка)?
- Инверсия (перестановка)
Перестано́вка — это упорядоченный набор чисел
 При этом n называется порядком перестановки. Число всех перестановок порядка n равно
При этом n называется порядком перестановки. Число всех перестановок порядка n равно 
Более общо, перестановкой произвольного (хотя обычно конечного) множества X называется биекция
 .
.Свойства
- Композиция определяет операцию произведения на перестановках
 Относительно этой операции множество перестановок образует группу, которую называют симметрической и обычно обозначают Sn (n — количество переставляемых элементов).
Относительно этой операции множество перестановок образует группу, которую называют симметрической и обычно обозначают Sn (n — количество переставляемых элементов). - Любая группа является подгруппой группы перестановок некоторого множества (например множества элементов этой группы). Каждый элемент
 сопоставляется с перестановкой
сопоставляется с перестановкой  где
где  — операция в группе G.
— операция в группе G.
Связанные определения
Специальные типы перестановок
Подстановки и произведения циклов
Перестановка π множества X может быть записана в виде подстановки, например:
где
 и π(xi) = yi.
и π(xi) = yi.Перестановку также можно записать в виде произведения непересекающихся циклов, причем единственным образом с точностью до порядка следования циклов в произведении. Например:
Случайная перестановка
Случайной перестановкой называется называется случайный вектор ξ = (ξ1,…,ξn), все элементы которого принимают натуральные значения от 1 до n, и при этом вероятность совпадения любых двух элементов равна 0.
Независимой случайной перестановкой называется такая случайная перестановка ξ, для которой
 для некоторых pij, для которых
для некоторых pij, для которых  и
и  Если при этом pij не зависят от i, то перестановку ξ называют одинаково распределённой. Если же нет зависимости от j, то есть
Если при этом pij не зависят от i, то перестановку ξ называют одинаково распределённой. Если же нет зависимости от j, то есть  то ξ называют однородной.
то ξ называют однородной.См. также
- Композиция определяет операцию произведения на перестановках
Wikimedia Foundation. 2010.
- Инверсия (лингвистика)
- Инверсия населенностей
Смотреть что такое «Инверсия (перестановка)» в других словарях:
Инверсия — В Викисловаре есть статья «инверсия» Инверсия: Инверсия в логике (от лат. inversio переворачивание, перестановка) переворачивани … Википедия
ИНВЕРСИЯ — (лат.). Превращение вообще и особенно превр. сахара в глюкозы и фруктозы. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ИНВЕРСИЯ [лат. inversio переворачивание, перестановка] 1) лингв. изменение обычного порядка… … Словарь иностранных слов русского языка
ИНВЕРСИЯ — (от лат. inversio – перестановка) в психологии объемно наглядное переворачивание. Напр., когда наблюдатель движется вперед и назад на некотором расстоянии перед маской, расположенной на темном фоне и обращенной к наблюдателю внутренней стороной,… … Философская энциклопедия
ИНВЕРСИЯ НАСЕЛЁННОСТЕЙ — (от лат. inversio переворачивание, перестановка), неравновесное состояние в ва, при к ром для составляющих его ч ц (атомов, молекул и т. п.) выполняется неравенство: N2/g2>N1/g1, где N2 и N1 населённости верх. и ниж. уровней энергии, g2 и g1 их… … Физическая энциклопедия
Инверсия — нарушение принятого в разговорной речи порядка слов и, тем самым, обычной интонации; последняя при И. характеризуется большим, чем обычно, числом пауз. При И. 1. слова меняются местами («Швейцара мимо он стрелой» Пушкин; «Или души задушены… … Литературная энциклопедия
ИНВЕРСИЯ — (лат. inversio переворачивание, перестановка) в психологии процесс и результат нарушения нормального порядка и последовательности элементов, их перестановка или замена вплоть до противоположных. Феномен И. распространяется на мотивы, установки,… … Новейший философский словарь
перестановка — изменение, переключение, коммутация, транспозиция, перемещение, перегруппировка, коммутирование; передвижение, перекомпоновка, передислокация, метатеза, гипертеза, смешивание, движение, анаграмма, перетаскивание Словарь русских синонимов.… … Словарь синонимов
ИНВЕРСИЯ НАСЕЛЁННОСТЕЙ — (от латинского inversio переворачивание, перестановка), неравновесное состояние вещества, при котором в отличие от обычного состояния теплового равновесия количество составляющих вещество частиц (атомов, молекул), находящихся на более высоких… … Современная энциклопедия
инверсия — обращение, инвертирование, изменение Словарь русских синонимов. инверсия сущ., кол во синонимов: 7 • гомосексуализм (23) • … Словарь синонимов
Инверсия населённостей — (от латинского inversio переворачивание, перестановка), неравновесное состояние вещества, при котором в отличие от обычного состояния теплового равновесия количество составляющих вещество частиц (атомов, молекул), находящихся на более высоких… … Иллюстрированный энциклопедический словарь
перестановка — Викисловарь
Морфологические и синтаксические свойства[править]
| падеж | ед. ч. | мн. ч. |
|---|---|---|
| Им. | перестано́вка | перестано́вки |
| Р. | перестано́вки | перестано́вок |
| Д. | перестано́вке | перестано́вкам |
| В. | перестано́вку | перестано́вки |
| Тв. | перестано́вкой перестано́вкою | перестано́вками |
| Пр. | перестано́вке | перестано́вках |
пе-ре-ста-но́в-ка
Существительное, неодушевлённое, женский род, 1-е склонение (тип склонения 3*a по классификации А. А. Зализняка).
Приставка: пере-; корень: -станов-; суффикс: -к; окончание: -а [Тихонов, 1996].
Произношение[править]
- МФА: [pʲɪrʲɪstɐˈnofkə]
Семантические свойства[править]
Значение[править]
- действие по значению гл. переставлять, перестанавливать; изменение расстановки, расположения чего-либо ◆ Отсутствует пример употребления (см. рекомендации).
- изменение порядка следования, замена одного другим ◆ Отсутствует пример употребления (см. рекомендации).
- результат таких изменений, новое расположение вещей, предметов ◆ Отсутствует пример употребления (см. рекомендации).
- матем., комбин. любой из вариантов упорядочения одного и того же набора неодинаковых объектов ◆ Сколько существует различных перестановок из 52 игральных карт?). Википедия
- матем., теор. гр. (для произвольного множества) биекция множества на себя, любой переход от одного варианта упорядочения к другому, то есть изменение порядка следования ◆ Любая группа является подгруппой группы перестановок некоторого множества (например множества элементов этой группы). Википедия
Синонимы[править]
- переконфигурация
- (иногда) подстановка
Антонимы[править]
- —
Гиперонимы[править]
- изменение
Гипонимы[править]
Родственные слова[править]
| Список всех слов с корнем «сто(j)-/ста-» | [править] | |
| ||
Этимология[править]
Происходит от гл. переставлять, из пере- + -ставлять (ставить), далее от праслав. *stāvītī, от кот. в числе прочего произошли: др.-русск. ставити, ст.-слав. ставити, ставлѭ (др.-греч. ἱστάναι, κωλύειν, στέλλειν), русск. ставить, укр. ста́вити, болг. ста́вя, сербохорв. ста̏вити, ста̏ви̑м, словенск. stáviti, stȃvim, чешск. staviti, словацк. stаvit᾽, польск. stawić, в.-луж. stawić, н.-луж. stawiś; восходит к праиндоевр. *stāw-. Родственно русск. став, далее — лит. stovė́ti, stóviu «стоять», латышск. stãve^t, готск. stojan «направлять», англос. stówian «удерживать», ср.-нж.-нем. stouwen, нов.-в.-нем. stauen «запруживать, задерживать», греч. στύ̄ω «поднимаю вверх». Сюда же лат. restaurāre «восстанавливать», īnstaurāre «возобновлять», греч. σταυρός «кол». Далее от праслав. *stati, от кот. в числе прочего произошли: др.-русск. стати, стану, ст.-слав. стати, станѫ (др.-греч. ἵστασθαι, γίγνεσθαι), русск. стать, стану, укр. ста́ти, ста́ну, сербохорв. ста̏ти, ста̏нем, словенск. státi, stȃnem «стать, стоить», чешск. stát sе «произойти, стать», словацк. stаť; восходит к праиндоевр. *stā- «стоять» Использованы данные словаря М. Фасмера. См. Список литературы.
Фразеологизмы и устойчивые сочетания[править]
Перевод[править]
| изменение порядка следования | |
| новый порядок, новое положение | |
| упорядоченный набор чисел | |
Библиография[править]
 | Для улучшения этой статьи желательно:
|
Перестановка — Википедия
6 перестановок 3 шаровВ комбинаторике перестано́вка — это упорядоченный набор без повторений чисел 1,2,…,n,{\displaystyle 1,2,\ldots ,n,} обычно трактуемый как биекция на множестве {1,2,…,n}{\displaystyle \{1,2,\ldots ,n\}}, которая числу i ставит в соответствие i-й элемент из набора. Число n при этом называется длиной перестановки[1].
В теории групп под перестановкой произвольного множества подразумевается биекция этого множества на себя. Как синоним слову «перестановка» в этом смысле некоторые авторы используют слово подстановка. (Другие авторы подстановкой называют наглядный способ записи перестановки.)
Свойства
- Pn=Ann=n!(n−n)!=n!0!=n!=1⋅2⋅⋯⋅n.{\displaystyle P_{n}=A_{n}^{n}={\frac {n!}{(n-n)!}}={\frac {n!}{0!}}=n!=1\cdot 2\cdot \dots \cdot n.}
Связанные определения
Специальные типы перестановок
- Тождественная перестановка — перестановка e,{\displaystyle e,} которая каждый элемент x∈X{\displaystyle x\in X} отображает в себя: e(x)=x.{\displaystyle e(x)=x.}
- Инволюция — перестановка τ,{\displaystyle \tau ,} которая является обратной самой себе, то есть τ⋅τ=e.{\displaystyle \tau \cdot \tau =e.}
- Беспорядок — перестановка без неподвижных точек.
- Циклом длины ℓ{\displaystyle \ell } называется такая подстановка π,{\displaystyle \pi ,} которая тождественна на всём множестве X,{\displaystyle X,} кроме подмножества {x1,x2,…,xℓ}⊂X{\displaystyle \{x_{1},x_{2},\dots ,x_{\ell }\}\subset X} и π(xℓ)=x1,π(xi)=xi+1.{\displaystyle \pi (x_{\ell })=x_{1},\pi (x_{i})=x_{i+1}.} Обозначается (x1,x2,…,xℓ).{\displaystyle (x_{1},x_{2},\dots ,x_{\ell }).}.
- Транспозиция — перестановка элементов множества X{\displaystyle X}, которая меняет местами два элемента. Транспозиция является циклом длины 2.
Подстановка
Перестановка π{\displaystyle \pi } множества X{\displaystyle X} может быть записана в виде подстановки, например:
- (x1x2x3…xny1y2y3…yn),{\displaystyle {\begin{pmatrix}x_{1}&x_{2}&x_{3}&\dots &x_{n}\\y_{1}&y_{2}&y_{3}&\dots &y_{n}\end{pmatrix}},}
где {x1,…,xn}={y1,…,yn}=X{\displaystyle \{x_{1},\dots ,x_{n}\}=\{y_{1},\dots ,y_{n}\}=X} и π(xi)=yi.{\displaystyle \pi (x_{i})=y_{i}.}
Произведения циклов и знак перестановки
Любая перестановка π{\displaystyle \pi } может быть разложена в произведение (композицию) непересекающихся циклов длины ℓ⩾2{\displaystyle \ell \geqslant 2}, причём единственным образом с точностью до порядка следования циклов в произведении. Например:
- (123456516423)=(1,5,2)(3,6).{\displaystyle {\begin{pmatrix}1&2&3&4&5&6\\5&1&6&4&2&3\end{pmatrix}}=(1,5,2)(3,6).}
Часто также считают, что неподвижные точки перестановки представляют собой самостоятельные циклы длины 1, и дополняют ими цикловое разложение перестановки. Для приведенного выше примера таким дополненным разложением будет (1,5,2)(3,6)(4){\displaystyle (1,5,2)(3,6)(4)}. Количество циклов разной длины, а именно набор чисел (c1,c2,…){\displaystyle (c_{1},c_{2},\dots )}, где cℓ{\displaystyle c_{\ell }} — это количество циклов длины ℓ{\displaystyle \ell }, определяет цикловую структуру перестановки. При этом величина 1⋅c1+2⋅c2+…{\displaystyle 1\cdot c_{1}+2\cdot c_{2}+\dots } равна длине перестановки, а величина c1+c2+…{\displaystyle c_{1}+c_{2}+\dots } равна общему количеству циклов. Количество перестановок из n элементов с k циклами даётся числом Стирлинга первого рода без знака [nk]{\displaystyle {\begin{bmatrix}n\\k\end{bmatrix}}}.
Любой цикл может быть разложен в произведение (не обязательно непересекающихся) транспозиций. При этом цикл длины 1 (являющийся по сути тождественной перестановкой e) можно представить как пустое произведение (англ.) транспозиций или, например, как квадрат любой транспозиции: (1,2)(1,2)=(2,3)(2,3)=e.{\displaystyle (1,2)(1,2)=(2,3)(2,3)=e.} Цикл длины ℓ⩾2{\displaystyle \ell \geqslant 2} можно разложить в произведение ℓ−1{\displaystyle \ell -1} транспозиций следующим образом:
- (x1,…,xl)=(x1,xℓ)(x1,xℓ−1)…(x1,x2).{\displaystyle (x_{1},\dots ,x_{l})=(x_{1},x_{\ell })(x_{1},x_{\ell -1})\dots (x_{1},x_{2}).}
Следует заметить, что разложение циклов на произведение транспозиций не является единственным:
- (1,2,3)=(1,3)(1,2)=(2,3)(1,3)=(1,3)(2,4)(2,4)(1,2).{\displaystyle (1,2,3)=(1,3)(1,2)=(2,3)(1,3)=(1,3)(2,4)(2,4)(1,2).}
Таким образом, любая перестановка может быть разложена в произведение транспозиций. Хотя это можно сделать многими способами, чётность количества транспозиций во всех таких разложениях одинакова. Это позволяет определить знак перестановки (чётностью перестановки или сигнатурой перестановки) π{\displaystyle \pi } как
- επ=(−1)t,{\displaystyle \varepsilon _{\pi }=(-1)^{t},}
где t{\displaystyle t} — количество транспозиций в каком-то разложении π{\displaystyle \pi }. При этом π{\displaystyle \pi } называют чётной перестановкой, если επ=1,{\displaystyle \varepsilon _{\pi }=1,} и нечётной перестановкой, если επ=−1.{\displaystyle \varepsilon _{\pi }=-1.}
Эквивалентно, знак перестановки определяется её цикловой структурой: знак перестановки π{\displaystyle \pi } из n{\displaystyle n} элементов, состоящий из k{\displaystyle k} циклов, равен
- επ=(−1)n−k.{\displaystyle \varepsilon _{\pi }=(-1)^{n-k}.}
Знак перестановки π{\displaystyle \pi } также может быть определен через количество инверсий N(π){\displaystyle N(\pi )} в π{\displaystyle \pi }:
- επ=(−1)N(π).{\displaystyle \varepsilon _{\pi }=(-1)^{N(\pi )}.}
Перестановки с повторением
Рассмотрим n элементов m различных типов, причем в каждом типе все элементы одинаковы. Тогда перестановки из всех этих элементов с точностью до порядка следования однотипных элементов называются перестановками с повторением. Если ki — количество элементов i-го типа, то k1+k2+⋯+km=n{\displaystyle k_{1}+k_{2}+\dots +k_{m}=n} и количество всевозможных перестановок с повторениями равно мультиномиальному коэффициенту (nk1, k2, …, km)=n!k1!k2!…km!.{\displaystyle \textstyle {\binom {n}{k_{1},\ k_{2},\ \dots ,\ k_{m}}}={\frac {n!}{k_{1}!k_{2}!\dots k_{m}!}}.}
Перестановку с повторениями можно также рассматривать как перестановку мультимножества {1k1,2k2,…,mkm}{\displaystyle \{1^{k_{1}},2^{k_{2}},\dots ,m^{k_{m}}\}} мощности k1+k2+⋯+km=n{\displaystyle k_{1}+k_{2}+\dots +k_{m}=n}.
Случайная перестановка
Случайной перестановкой называется случайный вектор ξ=(ξ1,…,ξn),{\displaystyle \xi =(\xi _{1},\ldots ,\xi _{n}),} все элементы которого принимают натуральные значения от 1 до n,{\displaystyle n,} и при этом вероятность совпадения любых двух элементов равна 0.
Независимой случайной перестановкой называется такая случайная перестановка ξ{\displaystyle \xi }, для которой
- P{ξ=σ}=p1σ(1)…pnσ(n)∑π∈Snp1π(1)…pnπ(n){\displaystyle P\{\xi =\sigma \}={\frac {p_{1\sigma (1)}\ldots p_{n\sigma (n)}}{\sum \limits _{\pi \in S_{n}}p_{1\pi (1)}\ldots p_{n\pi (n)}}}}
для некоторых pij,{\displaystyle p_{ij},} таких, что
- ∀i(1⩽i⩽n):pi1+…+pin=1{\displaystyle \forall i(1\leqslant i\leqslant n):p_{i1}+\ldots +p_{in}=1}
- ∑π∈Snp1π(1)…pnπ(n)>0.{\displaystyle \sum \limits _{\pi \in S_{n}}p_{1\pi (1)}\ldots p_{n\pi (n)}>0.}
Если при этом pij{\displaystyle p_{ij}} не зависят от i{\displaystyle i}, то перестановку ξ{\displaystyle \xi } называют одинаково распределённой. Если же нет зависимости от j{\displaystyle j}, то есть ∀i,j(1≤i,j≤n):pij=1/n,{\displaystyle \scriptstyle \forall i,j(1\leq i,j\leq n):p_{ij}=1/n,} то ξ{\displaystyle \xi } называют однородной.

 При этом n называется порядком перестановки. Число всех перестановок порядка n равно
При этом n называется порядком перестановки. Число всех перестановок порядка n равно 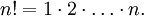
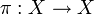 .
.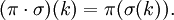 Относительно этой операции множество перестановок образует группу, которую называют симметрической и обычно обозначают Sn (n — количество переставляемых элементов).
Относительно этой операции множество перестановок образует группу, которую называют симметрической и обычно обозначают Sn (n — количество переставляемых элементов).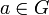 сопоставляется с перестановкой
сопоставляется с перестановкой 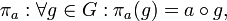 где
где  — операция в группе G.
— операция в группе G.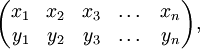
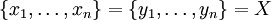 и π(xi) = yi.
и π(xi) = yi.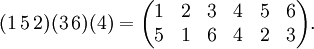
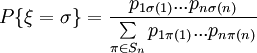 для некоторых pij, для которых
для некоторых pij, для которых 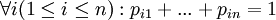 и
и 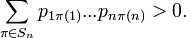 Если при этом pij не зависят от i, то перестановку ξ называют одинаково распределённой. Если же нет зависимости от j, то есть
Если при этом pij не зависят от i, то перестановку ξ называют одинаково распределённой. Если же нет зависимости от j, то есть 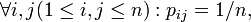 то ξ называют однородной.
то ξ называют однородной.