Как сделать восьмиугольник: Правильный восьмиугольник — Википедия – Как построить правильный восьмиугольник — Ответы на все вопросы — Антемион

Содержание

Правильный восьмиугольник — Википедия

Правильный восьмиугольник (октагон) — геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов, все углы и стороны равны между собой.

Правильный восьмиугольник имеет символ Шлефли {8} ^[1] и может быть построен также как квазиправильный усечённый квадрат, t{4}, в котором перемежаются два типа граней. Усечённый восьмиугольник (t{8}) является шестнадцатиугольником (t{16}).

Построение правильного восьмиугольника

Построение правильного 8-угольника путём складывания листа бумаги

Восьмиугольник можно построить проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.
Сумма всех внутренних углов правильного восьмиугольника составляет 1080°

Угол правильного восьмиугольника составляет 135∘{\displaystyle 135^{\circ }}

Формулы расчёта параметров правильного восьмиугольника[править | править код]

Пример:

t — длина стороны восьмиугольника
r — радиус вписанной окружности
R — радиус описанной окружности
S — площадь восьмиугольника
k — константа, равная (1+2){\displaystyle (1+{\sqrt {2}})} ≈ 2,414213562373095

Так как правильный восьмиугольник можно получить соответствующим отсечением углов квадрата со стороной kt{\displaystyle kt}, радиус вписанной окружности, радиус описанной окружности и площадь правильного восьмиугольника можно вычислить и без использования тригонометрических функций:

Радиус вписанной окружности правильного восьмиугольника:

r=k2t{\displaystyle r={\frac {k}{2}}t}

Радиус описанной окружности правильного восьмиугольника:

R=tkk−1{\displaystyle R=t{\sqrt {\frac {k}{k-1}}}}

Через сторону восьмиугольника

S=2kt2=2(1+2)t2≃4.828t2.{\displaystyle S=2kt^{2}=2(1+{\sqrt {2}})t^{2}\simeq 4.828\,t^{2}.}

Через радиус описанной окружности

S=4sin⁡π4R2=22R2≃2.828R2.{\displaystyle S=4\sin {\frac {\pi }{4}}R^{2}=2{\sqrt {2}}R^{2}\simeq 2.828\,R^{2}.}

Через апофему (высоту)

A=8tan⁡π8r2=8(2−1)r2≃3.314r2.{\displaystyle A=8\tan {\frac {\pi }{8}}r^{2}=8({\sqrt {2}}-1)r^{2}\simeq 3.314\,r^{2}.}

Площадь можно также вычислить как усечение квадрата

S=A2−a2,{\displaystyle S=A^{2}-a^{2},}

где A — ширина восьмиугольника (вторая меньшая диагональ), а a — длина его стороны. Это легко показать, если провести через противоположные стороны прямые, что даст квадрат. Легко показать, что угловые треугольники равнобедренные с основанием, равным a. Если их сложить (как на рисунке), получится квадрат со стороной a.

Если задана сторона a, то длина A равна

A=a2+a+a2=(1+2)a≈2.414a.{\displaystyle A={\frac {a}{\sqrt {2}}}+a+{\frac {a}{\sqrt {2}}}=(1+{\sqrt {2}})a\approx 2.414a.}

Тогда площадь равна:

S=((1+2)a)2−a2=2(1+2)a2≈4.828a2.{\displaystyle S=((1+{\sqrt {2}})a)^{2}-a^{2}=2(1+{\sqrt {2}})a^{2}\approx 4.828a^{2}.}

Площадь через A (ширину восьмиугольника)

S=2(2−1)A2≈0.828A2.{\displaystyle S=2({\sqrt {2}}-1)A^{2}\approx 0.828A^{2}.}

Ещё одна простая формула площади:

S=2aA.{\displaystyle \ S=2aA.}

Часто значение A известно, в то время как величину стороны a следует найти, как, например, при отрезании от квадратного куска материала углов с целью получения правильного восьмиугольника. Из формул выше имеем

a≈A/2.414.{\displaystyle a\approx A/2.414.}

Два катета углового треугольника можно получить по формуле

e=(A−a)/2.{\displaystyle e=(A-a)/2.}

$e=(A-a)/2.$ 11 симметрий правильного восьмиугольника. Линии зеркальных отражений показаны цветом — синие линии проходят через вершины, фиолетовые проходят через середины рёбер, число поворотов указано в центре. Вершины раскрашены согласно симметрии.

Правильный восьмиугольник имеет группу симметрии Dih₈ порядка 16. Имеется 3 диэдральные подгруппы — Dih₄, Dih₂ и Dih₁, а также 4 циклические подгруппы — Z₈, Z₄, Z₂ и Z₁. Последняя подгруппа подразумевает отсутствие симметрии.

Правильный восьмиугольник имеет 11 различных симметрий. Джон Конвей обозначил полную симметрию как r16 ^[2]. Диэдральные симметрии делятся на симметрии, проходящие через вершины (обозначены как d — от diagonal), или через рёбра (обозначены как p — от perpendiculars). Циклические симметрии в среднем столбце обозначены буквой g и для них указан порядок группы вращения. Полная симметрия правильного восьмиугольника обозначена как r16 а отсутствие — как a1.

На рисунке слева показаны типы симметрий восьмиугольников. Наиболее общие симметрии восьмиугольников — p8, равноугольный^[en] восьмиугольник, построенный четырьмя зеркалами и имеющий перемежающиеся длинные короткие стороны, и

d8, изотоксальный восьмиугольник, имеющий рёбра равной длины, но вершины имеют два разных внутренних угла. Эти две формы являются двойственным^[en] друг другу и имеют порядок, равный половине симметрии правильного восьмиугольника.

Каждая подгруппа симметрии даёт одну или более степеней свободы для неправильных форм. Только подгруппа g8 не имеет степеней свободы, но может рассматриваться как имеющая ориентированные рёбра.

Разрезание правильного восьмиугольника[править | править код]

Коксетер утверждает, что любой 2m-угольник с параллельными противоположными сторонами можно разрезать на m(m-1)/2 ромбов. Для восьмиугольника m=4 и он разрезается на 6 ромбов, как показано на рисунке ниже. Это разрезание можно рассматривать как 6 из 24 граней проекции многоугольника Петри тессеракта ^[3].

Разрезание правильного восьмиугольника
На 6 ромбов	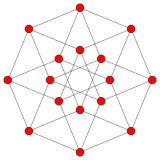Тессеракт

Восьмиугольный план Купола Скалы

В странах, принявших Венскую конвенцию о дорожных знаках и сигналах (в том числе в России), а также во многих других странах, знак «Движение без остановки запрещено» имеет вид красного восьмиугольника.

Восьмиугольные формы часто используются в архитектуре. Купол Скалы имеет восьмиугольный план. Башня Ветров в Афинах — ещё один пример восьмиугольной структуры. Восьмиугольный план встречается также в архитектуре церквей, таких как Собор Святого Георгия (Аддис-Абеба), Сан-Витале (в городе Равенна, Италия), Замок Кастель-дель-Монте (Апулия, Италия), Флорентийский баптистерий и восьмиугольные церкви Норвегии

[en]. Центральное пространство в Ахенский собор, Капелла Карла Великого имеют планы в виде правильного восьмиугольника.

Другие использования[править | править код]

Как построить правильный восьмиугольник — Ответы на все вопросы

Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.

Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.

Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.

Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны

1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.

Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.

Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.

Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.

Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°.

Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2.

Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

Построение вписанного в окружность правильного пятиугольника.

Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.

Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1.

Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5.

Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.

Построение правильного пятиугольника по данной его стороне.

Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.

Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.

Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Построение вписанного в окружность правильного семиугольника.

Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.

Приведённый способ годен для построения правильных многоугольников с любым числом сторон.

Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты. Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.

Источник: http://www.nacherchy.ru/postroenie_pravilnich_mnogougolnikov.html

Как самому сделать восьмиугольную беседку

Чтобы сделать любую беседку у себя на участке, нужно сначала определиться с местом, где она будет стоять, и подготовить его.
Итак, место выбрано и подготовлено.
Восьмиугольная беседка: разметка.

Прежде всего, нужно разметить правильный восьмиугольник. Как это сделать?

Нужно нарисовать квадрат, затем провести в нем диагонали.
Каждую сторону следует разделить пополам.
Через точку пересечения диагоналей и середину каждой стороны нужно провести отрезок, равный длине половины диагонали.
Теперь осталось последовательно соединить полученные точки и вершины квадрата.

восьмиугольная беседка

Восьмиугольная беседка: ставим столбики.

После построения правильного многоугольника в точки его вершин вбиваются столбики нужной высоты и плюс один, в точке пересечения диагоналей. Потом еще два столба, чтобы поддержать балки потом.

Каждый столбик нужно пробурить буром, например, диаметром 15 см на 90 см.

Туда втыкаются трубы с 15 см в диаметре, внутрь труб втыкается арматура так, чтобы она была выше уровня вставленной трубы. Затем арматура заливается цементным раствором.

Как только все застынет, обрезают болгаркой арматуру настолько, чтобы ее осталось выше уровня трубы 5 см. После этого собирается первая нижняя обвязка размером, как говорят, “вполдерева”.

Получится правильный восьмиугольник с внутренними параллельно расположенными балками.

На углах с помощью шкантов и шурупов ставят вертикальные столбики-стойки. Их примерное сечение 100 мм х70 мм. Их выбирают круглыми, квадратными или треугольными. Сверху них делается деревянная обвязка, обрезанная под таким углом, чтобы доски легли хорошо. Прикрепляется она к верхним торцовым концам стоек.

Восьмиугольная беседка: стропила.

Вырезается затем фанерный круг диаметром 35см (толщина фанеры может быть 20 мм). Круг прикрепляется к верху центральной вертикальной стойке. Затем из брусков делают стропила. Кладут каждый так: один конец на обвязку над вертикальными стойками, а другой конец кладут на круг. Стропила подгоняют, делая вырезы, чтобы легли хорошо.

Обрешетка, конечно, дело трудоемкое. Ведь нужно срезать доски обоих сторон под заданным углом 22,50, причем постараться сделать это максимально точно, чтобы они хорошо состыковались над стропилами. Эта работа является самой тонкой и кропотливой.

Восьмиугольная беседка: завершающие работы.

Пол можно застелить доской, обработав ее предварительно для выравнивания. Шпунтованные доски лучше не применять. В шпунтовые канавки может попадать дождевая вода, что приведет к гниению дерева. Пол хорошо бы обработать масляной краской.

Стол сделать можно таким образом: на вертикальной стойке, на уровне высоты стола вырезают канавку, чтобы круг получился, и такую же канавку вырезают внизу стойки. Стол выбирают диаметром примерно 150-180 см. Для стола можно подобрать 4 мебельных доски, сложить их вместе и вырезать круг. Затем нужно вырезать и середину по диаметру пояска, который был вырезан ранее.

Для укрепления стола берут 2 части десятимиллиметровой фанеры, вырезают круги диаметром 0,7 м, разрезают каждую часть еще на две равные части, и потом серединку делают. Положив их на пол вокруг стойки с некоторым смещением, стягивают шурупами.

Дальше делается столешница их приготовленных четырех частей.
Крышу тоже покрывают по своему усмотрению и с учетом материалов, которые наиболее доступны.
Восьмиугольная беседка

Источник: https://zelo.club/kak-samomu-sdelat-vosmiugolnuyu-besedku.html

как построить правильный восьмиугольник

ВАЖНО! Для того, что бы сохранить статью в закладки, нажмите: CTRL + D

Задать вопрос ВРАЧУ, и получить БЕСПЛАТНЫЙ ОТВЕТ, Вы можете заполнив на НАШЕМ САЙТЕ специальную форму, по этой ссылке >>>

В черчении зачастую требуется строить положительные многоугольники. Так, скажем, положительные восьмиугольники применяются на щитах дорожных знаков.

Инструкция

Для этого вначале постройте квадрат со стороной, равной отрезку, проведите в нем диагонали.

Сейчас постройте биссектрисы углов при диагоналях (на рисунке биссектрисы указаны синим), на пересечении биссектрис образуется вершина равнобедренного треугольника, стороны которого равны радиусу окружности, описанной вокруг верного восьмиугольника.

Верный треугольник — тот, у которого все стороны владеют идентичной длиной. Исходя из этого определения, построение сходственной разновидности треугольник а является нетрудной задачей.

Линейка, лист разлинованной бумаги, карандаш

Инструкция

1. Взять лист чистой бумаги, разлинованной в клеточку, линейку и подметить на бумаге три точки так, дабы они находились на идентичном друг от друга расстоянии (рис.1)

Восьмиугольник – это, по своей сути, два квадрата, смещенных касательно друг друга на 45° и объединенных на вершинах цельной линией.

А потому, для того дабы положительно изобразить такую геометрическую фигуру, нужно твердым карандашом дюже опрятно, по правилам начертить квадрат либо круг, с которыми и проводить последующие действия. Изложение ориентировано на длину стороны, равной 20 см.

А значит, при расположении чертежа рассматривайте, дабы вертикальная и горизонтальная линии длиной 20 см умещались на листе бумаги.

Линейка, прямоугольный треугольник, транспортир, карандаш, циркуль, лист бумаги

Инструкция

1. Метод 1. Начертите внизу горизонтальную линию длиной 20 см. После этого с одной стороны подметьте транспортиром прямой угол, тот, что составляет 90°.

То же самое дозволено сделать с поддержкой прямого треугольника. Проведите вертикальную линию и подметьте 20 см. Проделайте те же самые манипуляции с иной стороны. Объедините две полученные точки горизонтальной линией.

В итоге получилась геометрическая фигура – квадрат.

Верный восьмиугольник – это геометрическая фигура, у которой всякий угол составляет 135?, и все стороны между собою равны. Эта фигура дюже зачастую используется в архитектуре, к примеру, при постройке колон, а также при изготовлении дорожного знака STOP. Как же нарисовать положительный восьмиугольник?

Инструкция

1. Нарисуйте вначале квадрат. После этого проведите окружность так, дабы квадрат оказался внутри круга.

Сейчас проведите две осевые серединные линии квадрата – горизонтальную и вертикальную до пересечения с кругом.

Объедините прямыми отрезками точки пересечения осей с кругом и точки прикосновения описанной окружности с квадратом. Таким образом, получите стороны верного восьмиугольника.

как правильно расставить приоритеты

Источник: http://jprosto.ru/kak-postroit-pravilnyiy-vosmiugolnik/

Правильный восьмиугольник имеет символ Шлефли [1] и может быть построен также как квазиправильный усечённый квадрат, t, в котором перемежаются два типа граней. Усечённый восьмиугольник (t) является шестнадцатиугольником (t).

Содержание

Восьмиугольник можно построить проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.
Сумма всех внутренних углов правильного восьмиугольника составляет 1080°
Угол правильного восьмиугольника составляет 135 ∘ >

t — длина стороны восьмиугольника
r — радиус вписанной окружности
R — радиус описанной окружности
S — площадь восьмиугольника
k — константа, равная ( 1 + 2 ) >)> ≈ 2,414213562373095

Через сторону восьмиугольника

Площадь можно также вычислить как усечение квадрата

Если задана сторона a, то длина A равна
Тогда площадь равна:
Площадь через A (ширину восьмиугольника)
Ещё одна простая формула площади:
Часто значение A известно, в то время как величину стороны a следует найти, как, например, при отрезании от квадратного куска материала углов с целью получения правильного восьмиугольника. Из формул выше имеем
Два катета углового треугольника можно получить по формуле

Правильный восьмиугольник имеет группу симметрии Dih8 порядка 16. Имеется 3 диэдральные подгруппы — Dih5, Dih3 и Dih2, а также 4 циклические подгруппы — Z8, Z4, Z2 и Z1. Последняя подгруппа подразумевает отсутствие симметрии.

Правильный восьмиугольник имеет 11 различных симметрий. Джон Конвей обозначил полную симметрию как r16 [2] .

Диэдральные симметрии делятся на симметрии, проходящие через вершины (обозначены как d — от diagonal), или через рёбра (обозначены как p — от perpendiculars).

Циклические симметрии в среднем столбце обозначены буквой g и для них указан порядок группы вращения. Полная симметрия правильного восьмиугольника обозначена как r16 а отсутствие — как a1.

Источник: http://ru-wiki.org/wiki/%D0%9F%D1%80%D0%B0%D0%B2%D0%B8%D0%BB%D1%8C%D0%BD%D1%8B%D0%B9_%D0%B2%D0%BE%D1%81%D1%8C%D0%BC%D0%B8%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA

Содержание

Восьмиугольник можно построить проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.
Сумма всех внутренних углов правильного восьмиугольника составляет 1080°
Угол правильного восьмиугольника составляет 135 ∘ >

t — длина стороны восьмиугольника
r — радиус вписанной окружности
R — радиус описанной окружности
S — площадь восьмиугольника
k — константа, равная ( 1 + 2 ) >)> ≈ 2,414213562373095

Через сторону восьмиугольника

Площадь можно также вычислить как усечение квадрата

Если задана сторона a, то длина A равна
Тогда площадь равна:
Площадь через A (ширину восьмиугольника)
Ещё одна простая формула площади:
Часто значение A известно, в то время как величину стороны a следует найти, как, например, при отрезании от квадратного куска материала углов с целью получения правильного восьмиугольника. Из формул выше имеем
Два катета углового треугольника можно получить по формуле

Правильный восьмиугольник имеет 11 различных симметрий. Джон Конвей обозначил полную симметрию как r16 [2] .

Источник: http://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B0%D0%B2%D0%B8%D0%BB%D1%8C%D0%BD%D1%8B%D0%B9_%D0%B2%D0%BE%D1%81%D1%8C%D0%BC%D0%B8%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA

Правильный многоугольник – это многоугольник, у которого все стороны и углы равны между собой. Зная длину стороны правильного многоугольника и их количество можно найти все необходимые параметры. Периметр такого многоугольника равен произведению длины стороны a на общее их количество n. P=an

Формула площади правильного многоугольника, зная стороны, представляет собой произведение количества сторон и квадрата длины стороны, деленное на четыре тангенса угла, полученного делением 180 градусов на то же количество сторон. S=(na^2)/(4 tan⁡〖(180°)/n〗 )

В правильный многоугольник можно вписать окружность и описать окружность вокруг него. Радиусы внутренней и внешней окружности всецело зависят от длины стороны и их количества.

Чтобы найти радиус вписанной окружности правильного многоугольника, зная сторону, нужно разделить ее на два тангенса угла, полученного делением 180 градусов на количество сторон.

Радиус описанной окружности, в свою очередь, равен стороне, деленной еа два синуса того же угла. r=a/(2 tan⁡〖(180°)/n〗 ) R=a/(2 sin⁡〖(180°)/n〗 )

Угол правильного многоугольника зависит только от количества сторон и рассчитывается как 180 градусов, деленные на количество сторон, и умноженные на разность количества сторон и двух. α=(n-2) (180°)/n

Источник: http://geleot.ru/education/math/geometry/calc/regular_polygon/side

Правильный восьмиугольник имеет 11 различных симметрий. Джон Конвей обозначил полную симметрию как r16 [2] .

На рисунке слева показаны типы симметрий восьмиугольников.

Наиболее общие симметрии восьмиугольников — p8, восьмиугольник, построенный четырьмя зеркалами и имеющий перемежающиеся длинные короткие стороны, и d8, изотоксальный восьмиугольник, имеющий рёбра равной длины, но вершины имеют два разных внутренних угла. Эти две формы являются друг другу и имеют порядок, равный половине симметрии правильного восьмиугольника.

Каждая подгруппа симметрии даёт одну или более степеней свободы для неправильных форм. Только подгруппа g8 не имеет степеней свободы, но может рассматриваться как имеющая ориентированные рёбра.

Восьмиугольные формы часто используются в архитектуре. Купол Скалы имеет восьмиугольный план. Башня Ветров в Афинах — ещё один пример восьмиугольной структуры.

Восьмиугольный план встречается также в архитектуре церквей, таких как Собор Святого Георгия (Аддис-Абеба), Сан-Витале (в городе Равенна, Италия), Замок Кастель-дель-Монте (Апулия, Италия), Флорентийский баптистерий и .

Центральное пространство в Ахенский собор, Капелла Карла Великого имеют планы в виде правильного восьмиугольника.

Восьмиугольник в качестве усечённого квадрата, является первым в последовательности усечённых гиперкубов:

Восьмиугольник в качестве растянутого квадрата является первым в последовательности растянутых гиперкубов:

Источник: http://dir.md/wiki/%D0%9F%D1%80%D0%B0%D0%B2%D0%B8%D0%BB%D1%8C%D0%BD%D1%8B%D0%B9_%D0%B2%D0%BE%D1%81%D1%8C%D0%BC%D0%B8%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA?host=ru.wikipedia.org

Источник: https://pravilnoli.ru/kak-postroit-pravilnyj-vosmiugolnik

Как построить правильный восьмиугольник | Сделай все сам

Вам понадобится

– циркуль
– линейка
– карандаш

Инструкция

1. Пускай задан отрезок, равный длине стороны желанного восьмиугольника. Требуется возвести верный восьмиугольник. Первым шагом постройте равнобедренный треугольник на заданном отрезке, применяя отрезок, как основание. Для этого вначале постройте квадрат со стороной, равной отрезку, проведите в нем диагонали. Сейчас постройте биссектрисы углов при диагоналях (на рисунке биссектрисы указаны синим), на пересечении биссектрис образуется вершина равнобедренного треугольника, стороны которого равны радиусу окружности, описанной вокруг верного восьмиугольника.

2. Постройте окружность с центром в вершине треугольника. Радиус окружности равен стороне треугольника. Сейчас разведите циркуль на расстояние, равное величине заданного отрезка. Отложите это расстояние на окружности, начиная от всякого конца отрезка. Объедините все полученные точки в восьмиугольник.

3. Если же задана окружность, в которую должен быть вписан восьмиугольник, то построения будут еще проще. Постройте две перпендикулярные друг другу осевые линии, проходящие через центр окружности. На пересечении осевых и окружности получатся четыре вершины грядущего восьмиугольника. Осталось поделить расстояние между этими точками на дуге окружности напополам, дабы получить еще четыре вершины.

Верный треугольник – тот, у которого все стороны владеют идентичной длиной. Исходя из этого определения, построение сходственной разновидности треугольник а является нетрудной задачей.

Вам понадобится

Линейка, лист разлинованной бумаги, карандаш

Инструкция

2. С подмогой линейки объединить подмеченные на листе точки ступенчато, друг за ином так, как это показано на рисунке 2.

Обратите внимание!
В верном (равностороннем) треугольнике все углы равны 60 градусам.

Полезный совет
Равносторонний треугольник так же является и равнобедренным. Если треугольник равнобедренный, то это обозначает, что 2 из 3-х его сторон равны, а третья сторона считается основанием. Всякий положительный треугольник является равнобедренным, в то время как обратное заявление не правильно.

Восьмиугольник – это, по своей сути, два квадрата, смещенных касательно друг друга на 45° и объединенных на вершинах цельной линией. А потому, для того дабы положительно изобразить такую геометрическую фигуру, нужно твердым карандашом дюже опрятно, по правилам начертить квадрат либо круг, с которыми и проводить последующие действия. Изложение ориентировано на длину стороны, равной 20 см. А значит, при расположении чертежа рассматривайте, дабы вертикальная и горизонтальная линии длиной 20 см умещались на листе бумаги.

Вам понадобится

Линейка, прямоугольный треугольник, транспортир, карандаш, циркуль, лист бумаги

Инструкция

1. Метод 1. Начертите внизу горизонтальную линию длиной 20 см. После этого с одной стороны подметьте транспортиром прямой угол, тот, что составляет 90°. То же самое дозволено сделать с поддержкой прямого треугольника. Проведите вертикальную линию и подметьте 20 см. Проделайте те же самые манипуляции с иной стороны. Объедините две полученные точки горизонтальной линией. В итоге получилась геометрическая фигура – квадрат.

2. Для того дабы возвести 2-й (смещенный) квадрат, потребуется центр фигуры. Для этого поделите всякую сторону квадрата на 2 части. Объедините вначале 2 точки параллельных верхней и нижней сторон, а потом точки боковых сторон. Проведите через центр квадрата 2 прямые линии, перпендикулярные касательно друг друга. Начиная от центра, отмерьте на новых прямых длину по 10 см, что в результате даст 4 прямые линии. Объедините 4 полученные наружные точки между собой, в итоге чего получится 2-й квадрат. Сейчас всякую точку из 8 полученных углов объедините между собой. Таким образом, будет начерчен восьмиугольник.

3. Метод 2. Для этого потребуется циркуль, линейка и транспортир. От центра листа с поддержкой циркуля начертите круг диаметром 20 см (радиус 10 см). Через центральную точку проведите прямую линию. После этого начертите вторую перпендикулярную ей линию. То же самое дозволено исполнить с подмогой транспортира либо прямого треугольника. В итоге круг будет поделен на 4 равные части. Дальше всякий из секций поделите еще на 2 части. Для этого также дозволено воспользоваться транспортиром, отмеряя 45° либо прямоугольным треугольником, тот, что приложите острым углом в 45° и проведите лучи. От центра на всякой прямой линии отмерьте по 10 см. В итоге получатся 8 «лучиков», которые объедините между собой. В итоге получится восьмиугольник.

4. Метод 3. Для этого так же начертите круг, проведите через середину линию. После этого возьмите транспортир, поставьте его на центр и отмеряйте углы, рассматривая, что всякий секция восьмиугольника имеет в центре угол 45° . Позже этого на полученных лучах отмерьте длину в 10 см. и объедините их между собой. Восьмиугольник готов.

Полезный совет
Делайте чертеж твердым карандашом, побочные линии на котором после этого легко дозволено будет удалить

Вам понадобится

– альбомный лист;
– карандаш;
– линейка;
– циркуль;
– ластик.

Инструкция

1. Нарисуйте вначале квадрат. После этого проведите окружность так, дабы квадрат оказался внутри круга. Сейчас проведите две осевые серединные линии квадрата – горизонтальную и вертикальную до пересечения с кругом. Объедините прямыми отрезками точки пересечения осей с кругом и точки прикосновения описанной окружности с квадратом. Таким образом, получите стороны верного восьмиугольника.

2. Нарисуйте верный восьмиугольник иным методом. Вначале начертите окружность. После этого проведите горизонтальную линию через ее центр. Подметьте точку пересечения крайней правой границы окружности с горизонталью. Эта точка будет являться центром еще одной окружности, радиусом равным предыдущей фигуре.

3. Проведите вертикальную линию через точки пересечения 2-й окружности с первой. Поставьте ножку циркуля в точку пересечения вертикали с горизонталью и начертите небольшой круг радиусом, равным расстоянию от центра крошечной окружности до центра начального круга.

4. Начертите прямую линию через две точки – центр начального круга и точку пересечения вертикали и крошечной окружности. Продолжите ее до пересечения с рубежом изначальной фигуры. Это будет точка вершины восьмиугольника. Циркулем подметьте еще одну точку, проведя окружность с центром в точке пересечения крайней правой рубежом начального круга с горизонталью и радиусом, равным расстоянию от центра к теснее имеющейся вершине восьмиугольника.

5. Проведите прямую линию через две точки – центр начального круга и последнюю новообразованную точку. Продолжите прямую линию до пересечения с границами первоначальной фигуры.

6. Объедините прямыми отрезками ступенчато: точку пересечения горизонтали с правой рубежом начальной фигуры, после этого по часовой стрелке все образовавшиеся точки, включая точки пересечения осей с первоначальной окружностью.

Видео по теме

Как самому сделать восьмиугольную беседку

Чтобы сделать любую беседку у себя на участке, нужно сначала определиться с местом, где она будет стоять, и подготовить его.

Итак, место выбрано и подготовлено.

Восьмиугольная беседка: разметка.

Прежде всего, нужно разметить правильный восьмиугольник. Как это сделать?

Нужно нарисовать квадрат, затем провести в нем диагонали.
Каждую сторону следует разделить пополам.
Через точку пересечения диагоналей и середину каждой стороны нужно провести отрезок, равный длине половины диагонали.
Теперь осталось последовательно соединить полученные точки и вершины квадрата.

восьмиугольная беседка

Восьмиугольная беседка: ставим столбики.

Каждый столбик нужно пробурить буром, например, диаметром 15 см на 90 см.

Туда втыкаются трубы с 15 см в диаметре, внутрь труб втыкается арматура так, чтобы она была выше уровня вставленной трубы. Затем арматура заливается цементным раствором. Как только все застынет, обрезают болгаркой арматуру настолько, чтобы ее осталось выше уровня трубы 5 см. После этого собирается первая нижняя обвязка размером, как говорят, «вполдерева». Получится правильный восьмиугольник с внутренними параллельно расположенными балками.

Восьмиугольная беседка: стропила.

Обрешетка, конечно, дело трудоемкое. Ведь нужно срезать доски обоих сторон под заданным углом 22,50, причем постараться сделать это максимально точно, чтобы они хорошо состыковались над стропилами. Эта работа является самой тонкой и кропотливой.

Восьмиугольная беседка: завершающие работы.

Дальше делается столешница их приготовленных четырех частей.

Крышу тоже покрывают по своему усмотрению и с учетом материалов, которые наиболее доступны.

Восьмиугольная беседка

Построение на плоскости | Журнал Ярмарки Мастеров

Наверняка каждому из нас приходилось сталкиваться с тем, что нужно срочно что-то начертить, точный угол или многоугольник, а транспортира как нарочно под рукой нет, или Вы вообще никогда раньше ничего не чертили. Сегодня я хочу поделиться с Вами простыми схемами построения фигур на плоскости. Думаю, этот навык пригодится всем. Продолжение статьи:
http://www.livemaster.ru/topic/383001-postroenie-na-ploskosti-chast-2?inside=1&wf=&cp=1&vr=1

Нам понадобятся: карандаш, линейка, циркуль.

Построение угла в 60

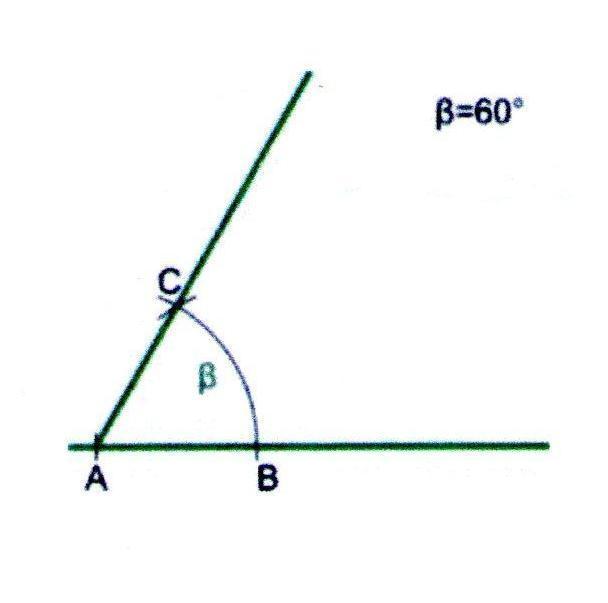
1. Проведём прямую и отметим на ней точку А.

2. Из точки А проведём дугу произвольного радиуса и получим точку В.

3. Из точки В проведём дугу радиуса АВ, чтобы она пересекла ранее начерченную дугу.

4. Проведённая через точку пересечения (С) и точку А прямая будет второй стороной требуемого угла.

Построение угла в 45

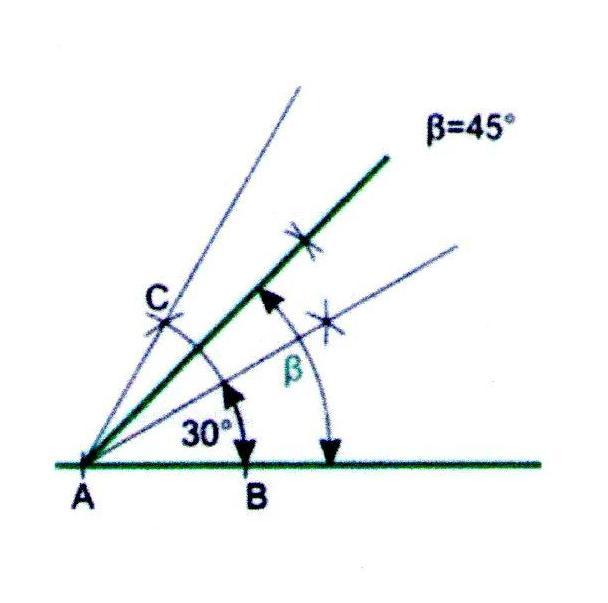1. Построим угол 60, кака описано выше.

2. Разделим полученный угол пополам.

3. Угол между лучами 60 и 30 разделим пополам. В результате получим угол в 45.

Построение угла в 75

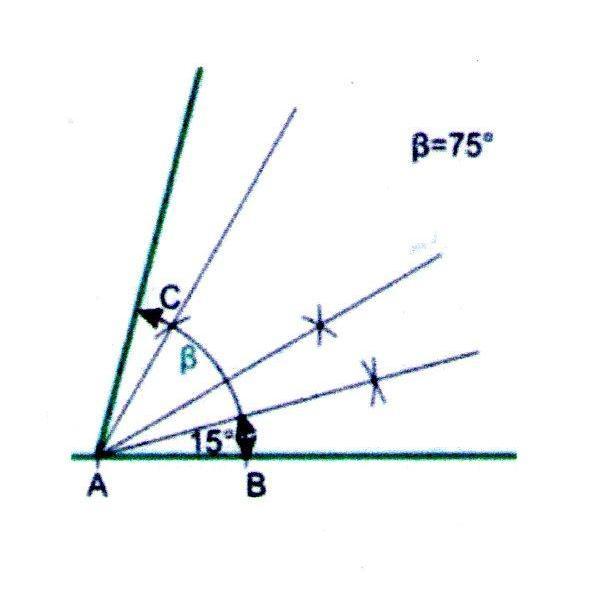1. Построим угол в 60, как описано выше, и разделим его пополам.

2. В ходе дальнейшего деления надвое получим угол в 15.

3. Отразим угол в 15 через луч 60 и так получим угол в 75.

Построение угла в 90

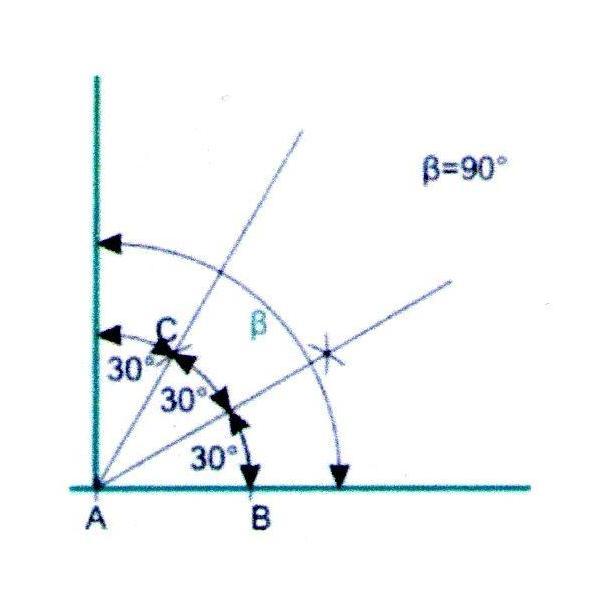
1. Построим угол в 60, как описано выше, и разделим его пополам.

2. Получившийся угол в 30 через луч 60 и так получим угол точно в 90.

Разделение отрезка на равные части.

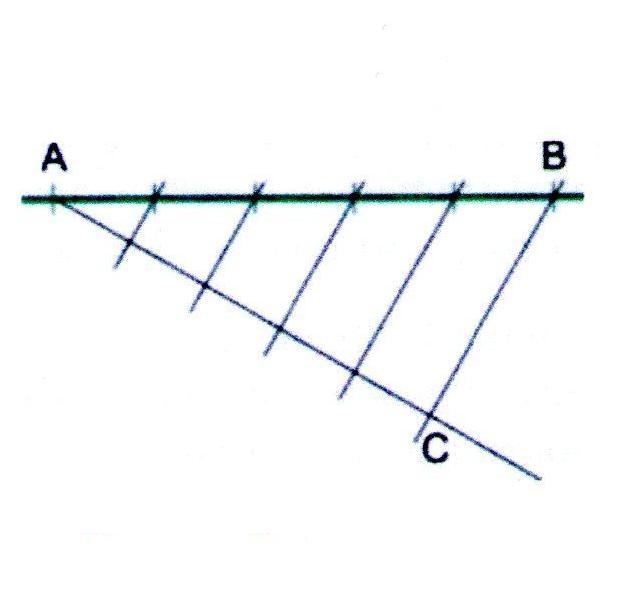
1. Проведём прямую и отметим на ней отрезок АВ.

2. Из точки А проведём вспомогательную прямую и разделим её на столько одинаковых частей, на сколько требуется разделить отрезок АВ. Делить будем при помощи циркуля. Последнюю точку обозначим буквой С.

3. Последнюю точка (С) соединим с концом отрезка АВ. Построим рад параллельных отрезку СВ прямых по всей длине отрезка АВ. Точки пересечения параллельных прямых с отрезком АВ и будут точками раздела отрезка на несколько равных частей.

Построение правильного пятиугольника.

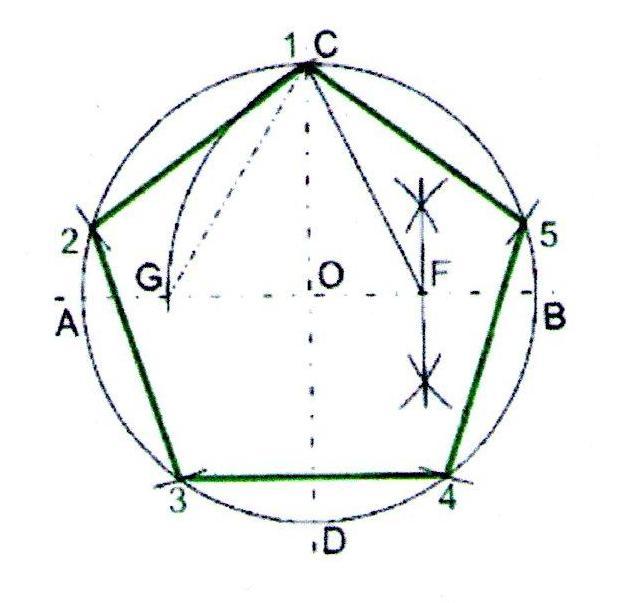
1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.

2. Разделим пополам расстояние ОВ. Разведём ножки циркуля на расстояние FC. Из точки F проведём дугу через С. Дуга пересечёт горизонтальную линию в точке G.

3. Расстояние CG будет длиной стороны пятиугольника. Из вершины С отложим пять раз расстояние CG.

Построение правильного шестиугольника.

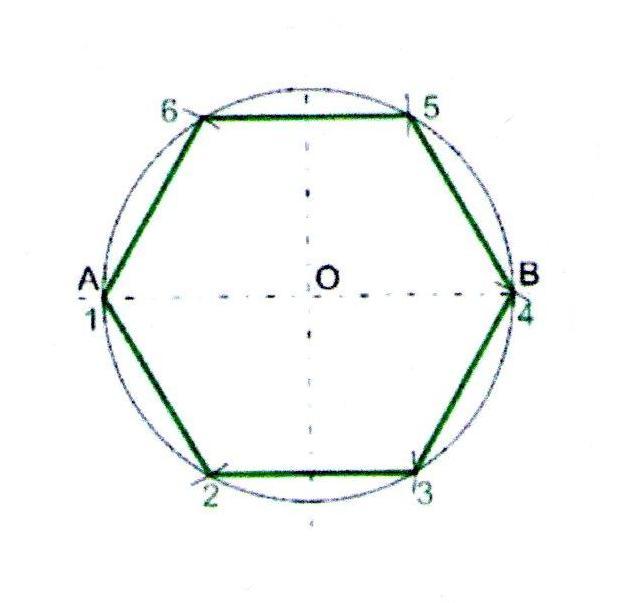
1. Проведём окружность радиусом 50 мм.

2. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.

3. Из точки А на линии окружности отложим шесть раз радиус нашей окружности. Соединив прямыми точки пересечения, получим шестиугольник.

Построение правильного семиугольника.

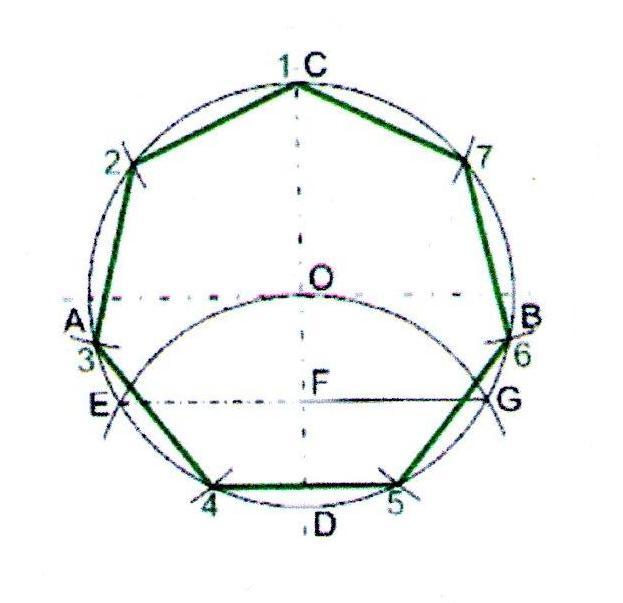
1. Проведём окружность заданного радиуса. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.

2. Из точки D проведём дугу радиусом равным радиусу окружности.

3. Дуга пересечёт окружность в точках E и G.

4. Длина отрезка EF на хорде EG равна длине стороны семиугольника. Из вершины С семь раз отложим расстояние EF.

Общий метод построения многоугольников.

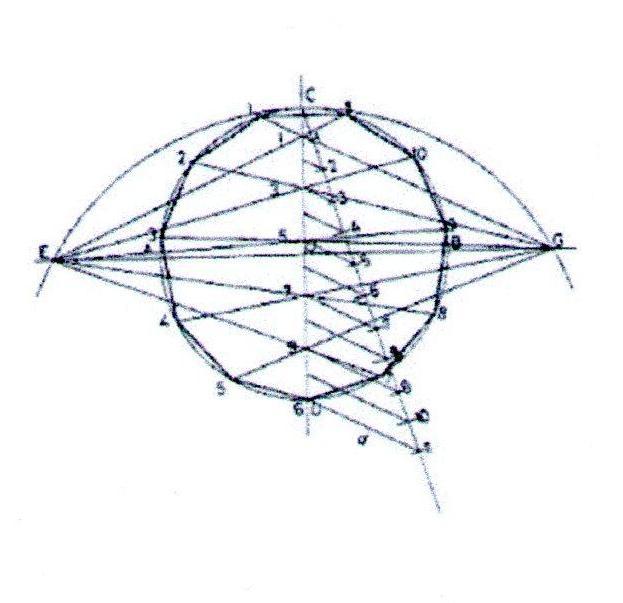
1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии. Продолжим горизонтальную лини. За точки А и В.

2. Из точки D проведём дугу радиусом, равным радиусу окружности так, чтобы дуга пересекла горизонтальную линию.

3. При помощи вспомогательной прямой разделим вертикальную линию на столько равных частей, сколько сторон многоугольника требуется получить. Для примера показано построение одиннадцатиугольника.

4. Из точки Е проведём прямые через нечётные точки раздела вертикальной линии так, чтобы эти прямые пересекли окружность. Такую же операцию проведём из точки G. Полученные лучи пересекают окружность в точках, соединив которые прямыми получаем одиннадцатиугольник.

Как построить восьмиугольник

Любой правильный многоугольник можно вписать в окружность. Поэтому при построении правильного восьмиугольника логично начать с окружности, которая послужит вспомогательной фигурой. Все вершины восьмиугольника будут лежать на этой линии.

При помощи циркуля проведите окружность. Отметьте ее центр.

Сделайте отметки на концах любого диаметра окружности. Это первые две вершины будущего восьмиугольника.

Установите раствор циркуля, равный диаметру окружности. Поставив иглу циркуля в одну из отмеченных на предыдущем этапе точек, сделайте засечки выше и ниже окружности. Старайтесь делать их не слишком короткими, поскольку они должны будут пересекаться с засечками, которые вы сделаете на следующем этапе.

Поставьте иглу циркуля в другую отмеченную точку и точно так же сделайте засечки выше и ниже окружности. Если провести прямую линию между точками пересечения засечек, то она пройдет через центр окружности, разделив первоначальный диаметр точно пополам, и будет к нему перпендикулярна.

Приложите линейку к двум найденным точкам и сделайте отметки на окружности там, где ее пересекает построенный перпендикуляр. Вы разделили окружность на четыре равные части, и найденные вами точки являются вершинами квадрата, вписанного в окружность. Первоначальный диаметр и его перпендикуляр, найденный на предыдущем этапе, служат диагоналями этого квадрата.

Чтобы завершить построение правильного восьмиугольника, нужно найти перпендикуляры к сторонам квадрата.

Установите раствор циркуля, равный стороне квадрата. Поместите иглу циркуляв любую вершину квадрата и сделайте засечки по обеим ее сторонам вне окружности.

Повторите процедуру с двумя вершинами квадрата, смежными с первой. У вас должны получиться две точки в местах пересечения засечек.

Приложите линейку так, чтобы она проходила через любую из найденных точек и центр окружности. Сделайте две отметки на окружности там, где ее пересекает полученная прямая. Повторите то же самое со второй найденной точкой. Теперь у вас есть восемь точек, делящих окружность на восемь равных частей. Это и есть вершины правильного восьмиугольника.

При помощи линейки соедините последовательно все восемь найденных точек. Построение завершено.

Что-то я туплю.. Как начертить правильный восьмиугольник по стороне?

При помощи циркуля проведите окружность. Отметьте ее центр.

Сделайте отметки на концах любого диаметра окружности. Это первые две вершины будущего восьмиугольника.

Чтобы завершить построение правильного восьмиугольника, нужно найти перпендикуляры к сторонам квадрата.

Установите раствор циркуля, равный стороне квадрата. Поместите иглу циркуля в любую вершину квадрата и сделайте засечки по обеим ее сторонам вне окружности.

При помощи линейки соедините последовательно все восемь найденных точек. Построение завершено.

Правильный восьмиугольник — Википедия

Формулы расчёта параметров правильного восьмиугольника[править | править код]

Разрезание правильного восьмиугольника[править | править код]

Другие использования[править | править код]

Как построить правильный восьмиугольник — Ответы на все вопросы

Как самому сделать восьмиугольную беседку

как построить правильный восьмиугольник

Инструкция

Инструкция

Инструкция

Инструкция

Содержание

Содержание

Как построить правильный восьмиугольник | Сделай все сам

Инструкция

Инструкция

Инструкция

Инструкция

Как самому сделать восьмиугольную беседку

Построение на плоскости | Журнал Ярмарки Мастеров

Как построить восьмиугольник

Что-то я туплю.. Как начертить правильный восьмиугольник по стороне?

Leave a Reply Отменить ответ